Consider a 3-dimensional Euclidean Space with 3 points :
1)(3,6,2)
It can be written as:
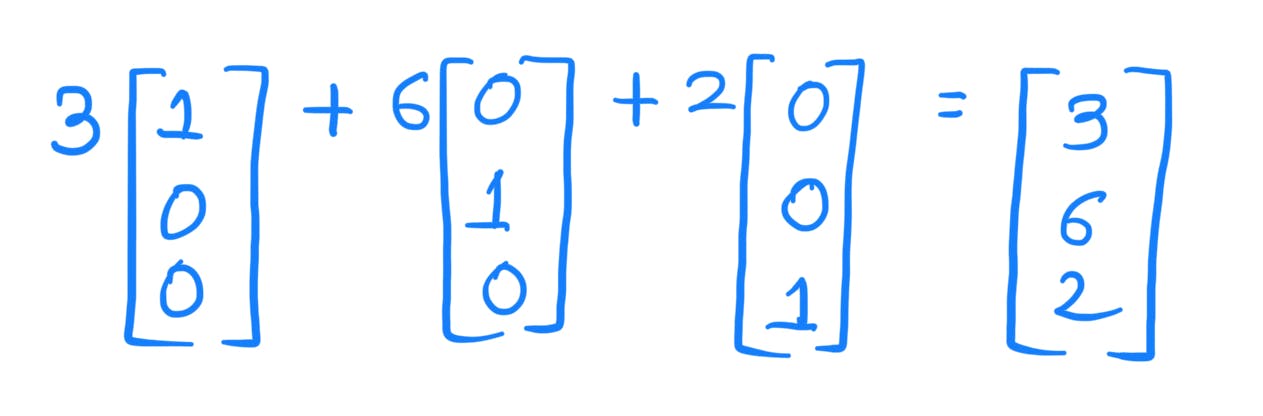
2)(-8,5,12)
It can be written as:

Any arbitrary point (a,b,c) can be expressed as :
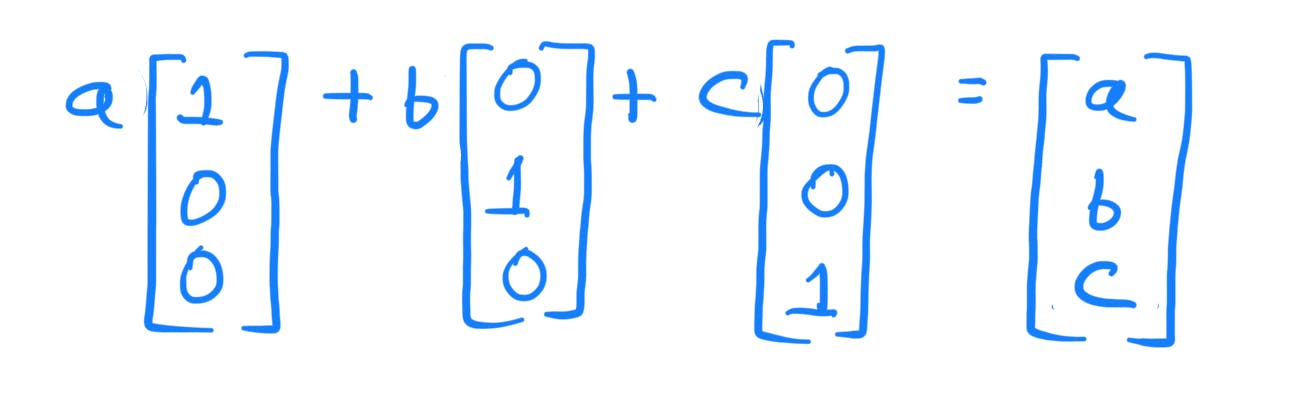
The 3 vectors :

can be used to express any point in the Euclidean space. These vectors span the entire Euclidean space. These are also called the basis set or spanning set.
A spanning set for a vector space is a set of vectors
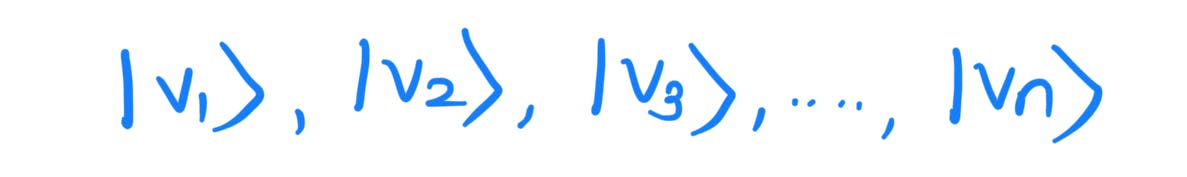
such that any vector |v> in the vector space can be written as

The number of vectors in the spanning set or the cardinality of the spanning set gives the dimension of the vector space.
For example, a spanning set for the vector space

is given by:
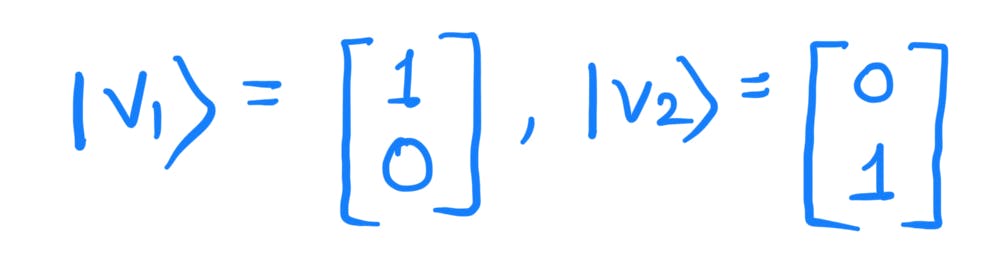
Any vector in the complex space

can be given as a linear combination of |v1> and |v2>.

Hence we say that the vectors |v1> and |v2> span the vector space complex space.
A vector space may have different spanning sets. A second spanning set for the same complex vector space is

Now a vector |v> can be expressed as:

Substituting and Expanding:

Hence for the second type of spanning set any arbitrary vector |v> = (a1,a2) can be written as a linear combination of |v1> and |v2> as below:

A set of non-zero vectors
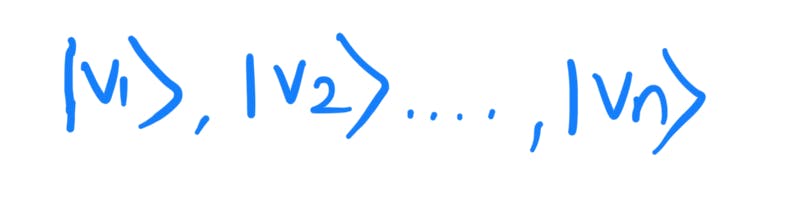
are linearly dependent if there exists a set of complex numbers
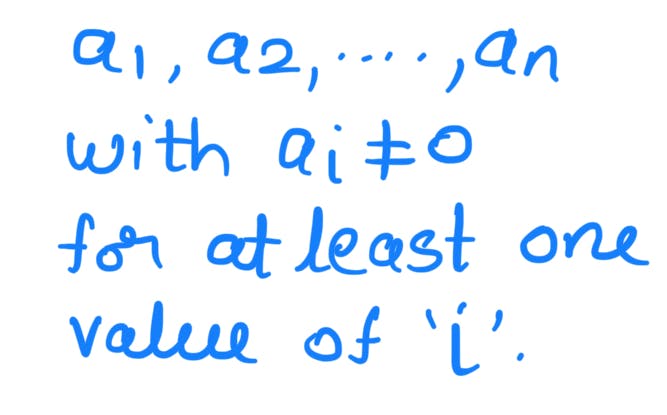
such that

For example:
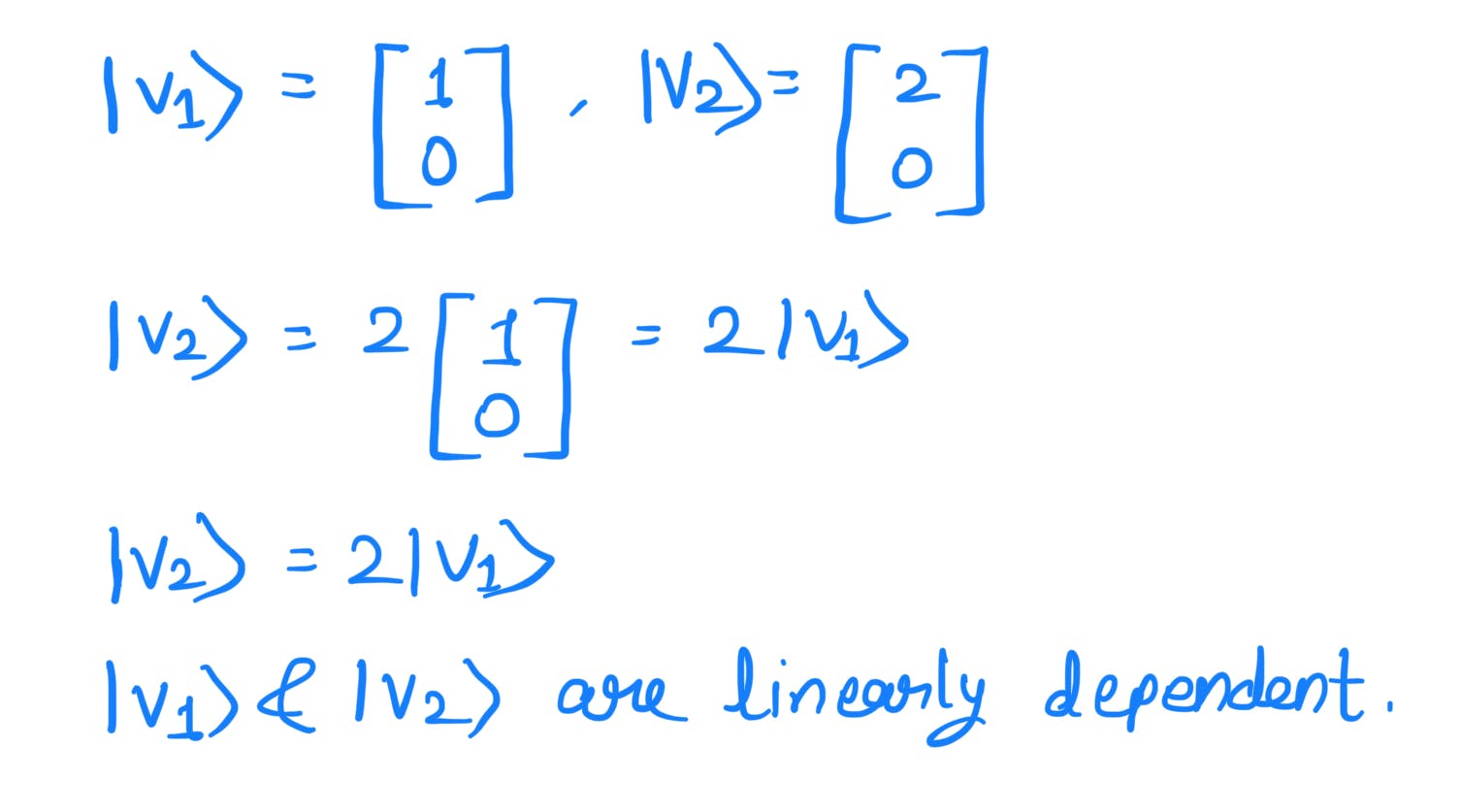
A set of vectors is linearly independent if it is not linearly dependent. The vectors in the spanning set are linearly independent.
Any two sets of linearly independent vectors that span a vector space V contain the same number of elements. These are called different bases for V.
Example:

The number of elements or the cardinality of the basis set is called the dimension of the vector space.
Such a basis set always exists. For now, we will only focus on finite-dimensional vector spaces.
Dimension of a Vector Space:
Consider the vector space

Any set of more than three vectors in the above space is linearly dependent.
Any set of less than three vectors in the above space does not span the space.
Any basis for the above space must have exactly three vectors.
Consider a set of polynomials with degree <= 2.

The basis set for above is given as :

Since there are 3 elements in the basis set the dimension of the above polynomial set=3
Let's solve one interesting question:
What is the dimension of the below set?
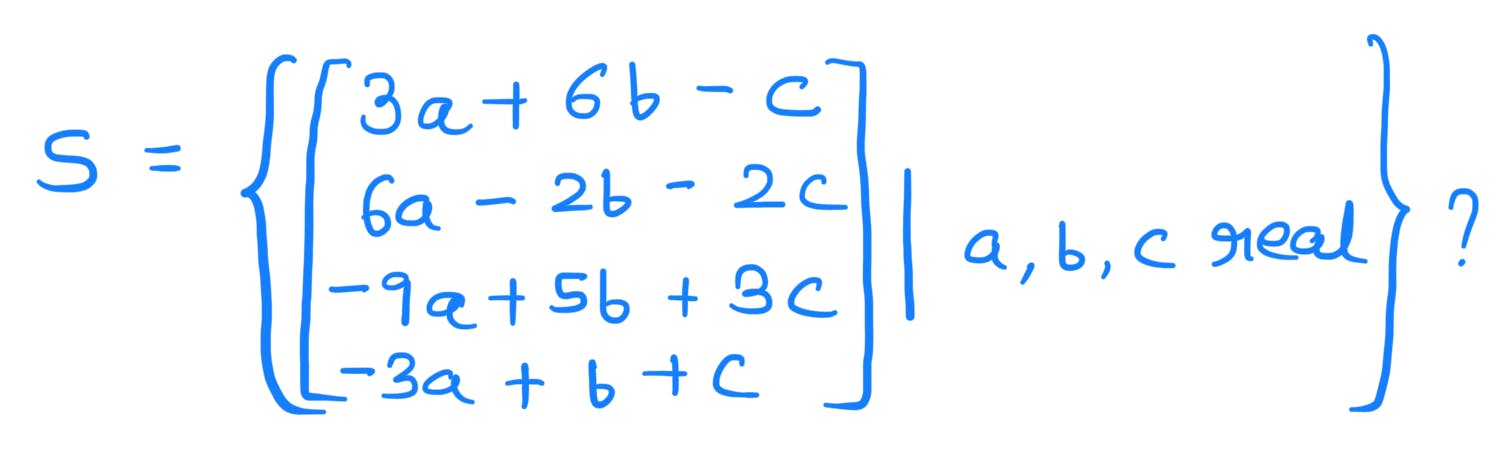
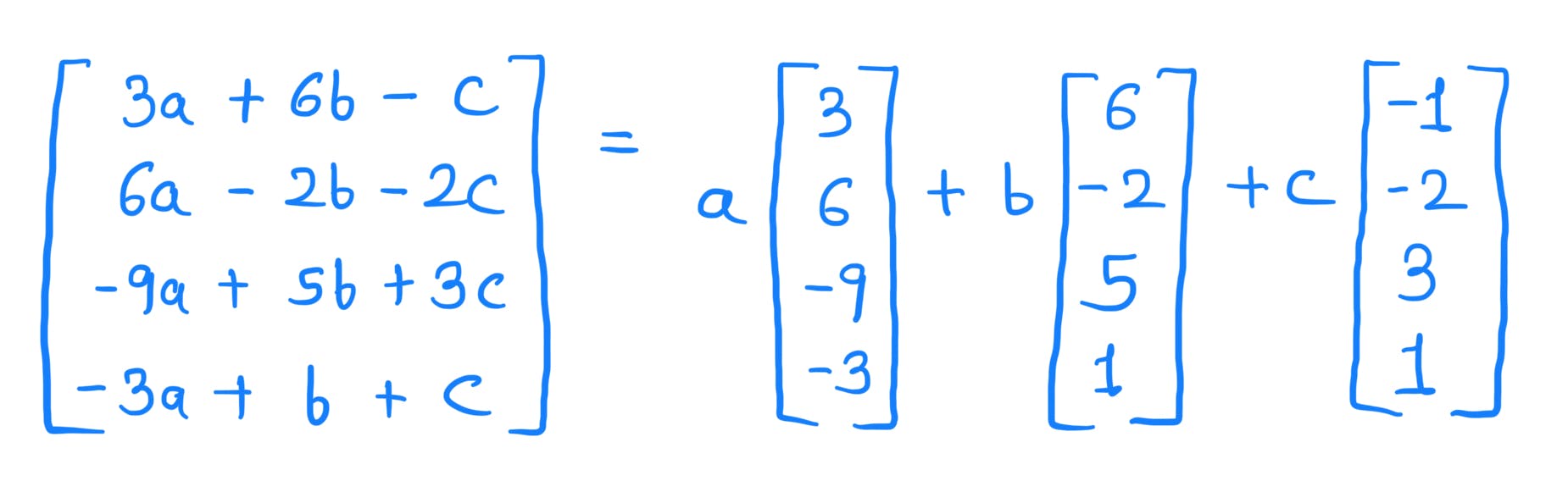
Now there are three vectors. The linearly independent vectors will be in the basis set. Write vectors in matrix form.
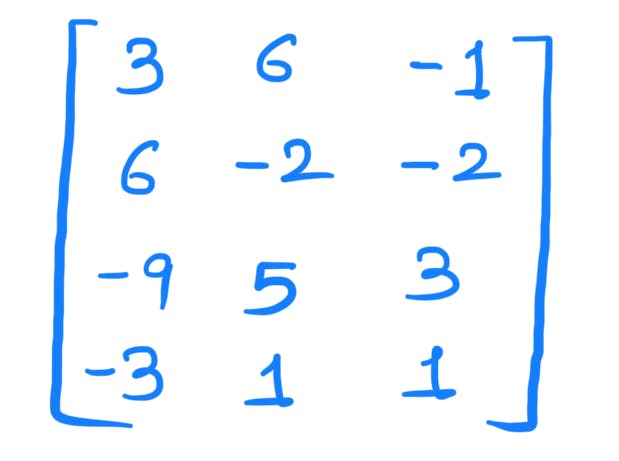
Convert in Row-Echelon form
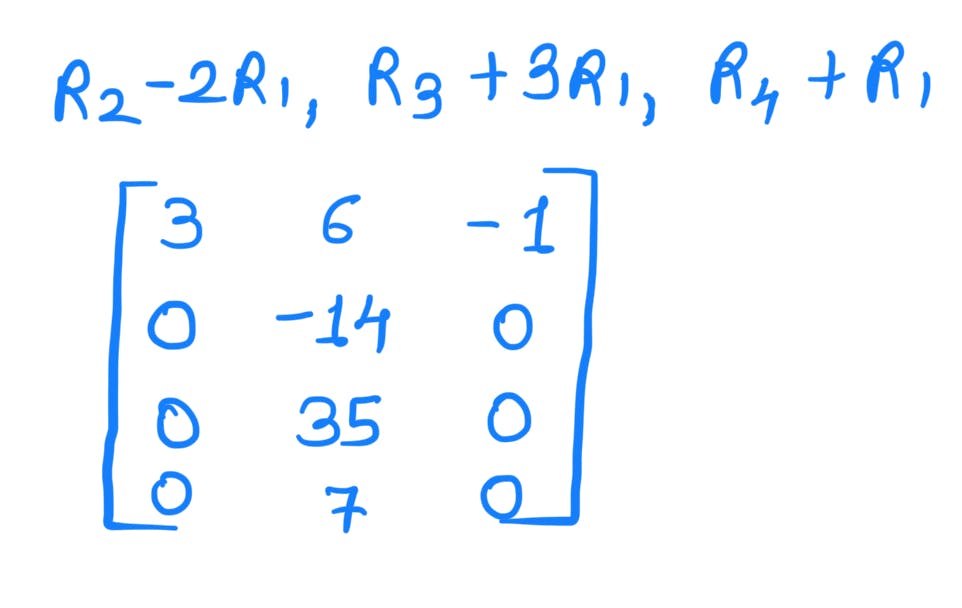
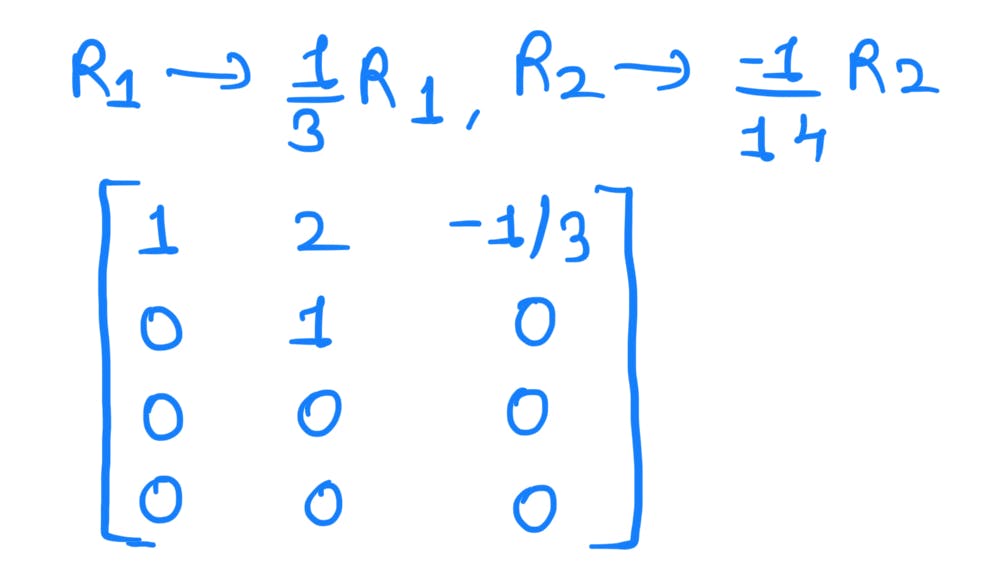

Column 1 and 2 consists of '1' and all other elements '0'. However, column 3 consists of -1/3. Hence columns 1 and 2 are linearly independent while column 3 is linearly dependent on column 1 with a factor of '-1/3'.
So a basis set would be :
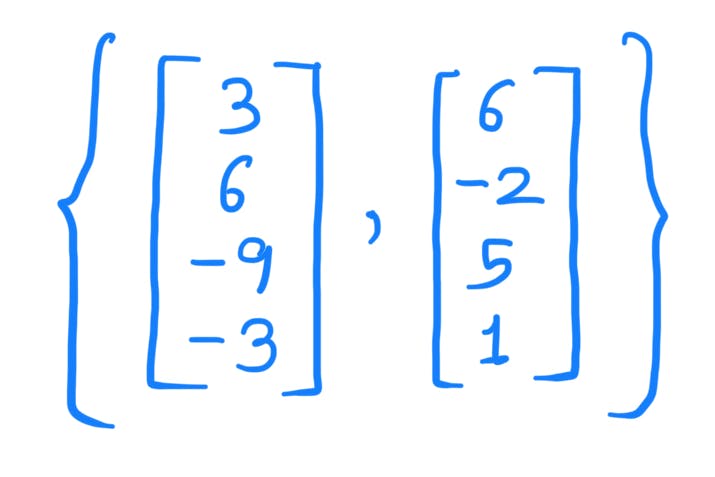
Dimension of the S = Number of elements in the basis set = 2
However the number of elements in each vector = 4.

The Basis Theorem:
If V is a n-dimensional vector space with n>=1 then:
Any linearly independent set of exactly n elements in V is automatically a basis for V.
Any set of exactly n elements that spans V is automatically a basis for V.
Conclusion:
Hence in the above blog, we studied
What are bases in Euclidean Space?
Spanning set in complex space
Different spanning sets of the same vector space.
Linearly Independent and Dependent Set of Vectors
Dimension of Vector Space
Credit for the above blog:
I have gained the information for the above blog from the book "Quantum Computing and Quantum Information" by Michael A. Nielsen and Isaac L. Chuang and a YouTube video by "Linear Algebra - Dimension of a Vector Space" by Betty Love. Link: https://www.youtube.com/watch?v=HCpUHRxc6F4
