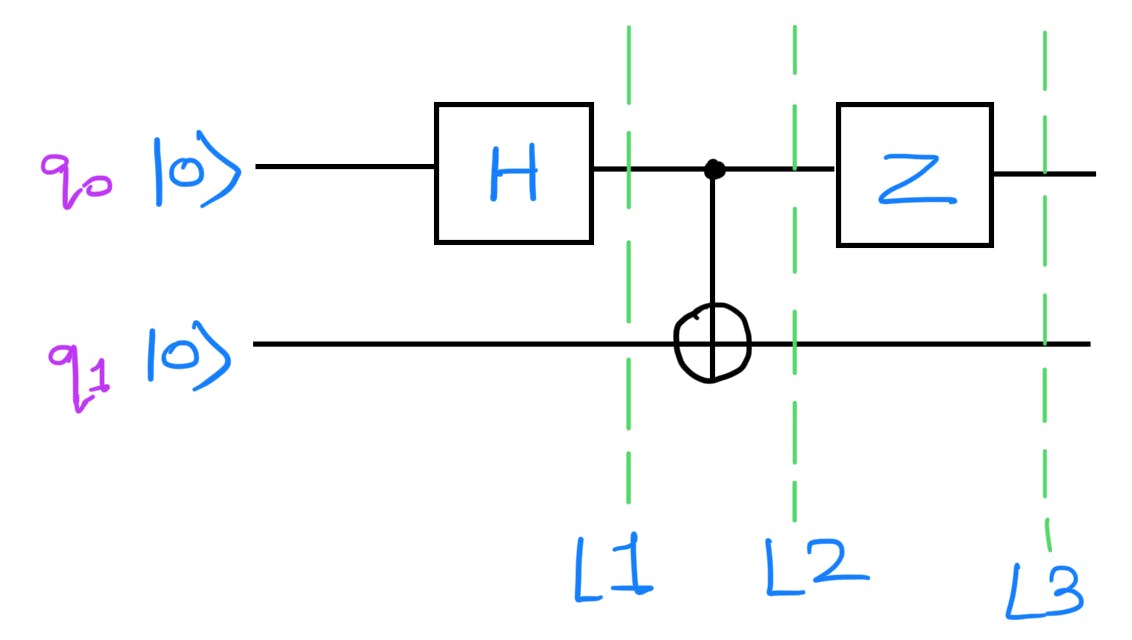
Consider a circuit that has a Hadamard Gate followed by a CNOT gate:

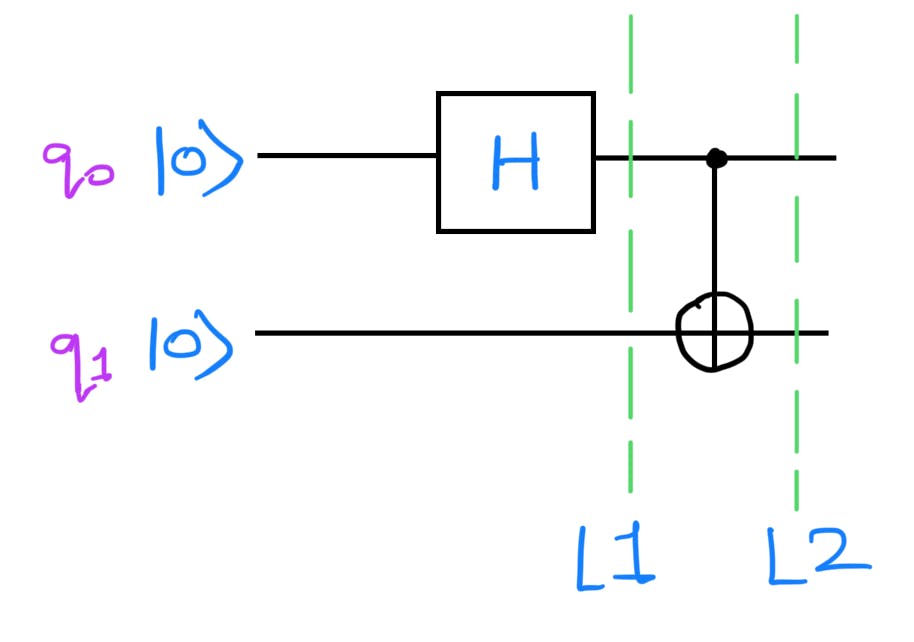
After applying the Hadamard Gate the quantum state of the circuit at L1 becomes(Using right-to-left ordering):

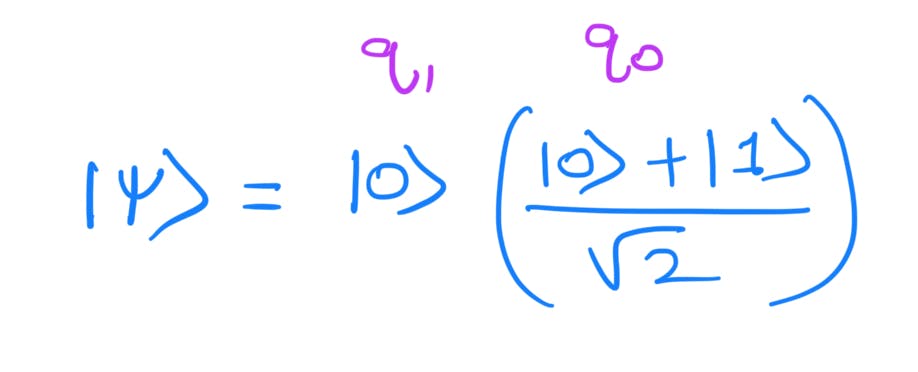
Then apply the CNOT gate where the control qubit is q0 and and target gate is q1. So quantum state at L2:

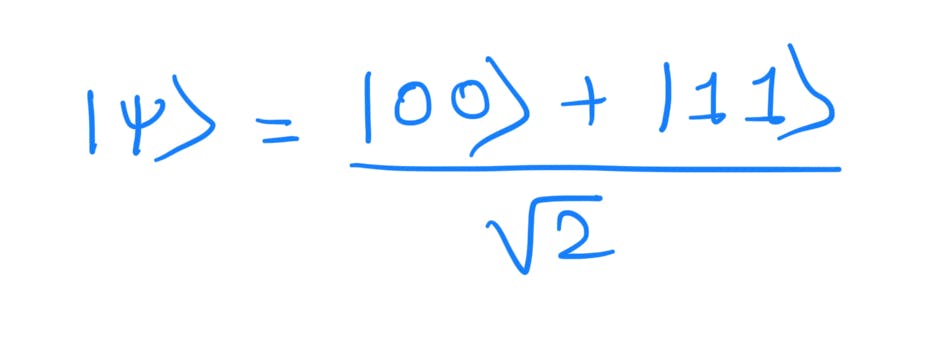
This is a special kind of quantum state where the state of one qubit determines the state of another. This is the mathematical definition of entanglement. Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in such a way that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance.

The above state has some special notations which we will discuss later in this blog.

Any entangled quantum state cannot be described as a tensor product of two quantum states OR Any entangled quantum state cannot be factorized.

Proof:

Let's say that the above-entangled state can be factorized into two quantum states

|Ψ⟩=a|0⟩+b|1⟩ and |φ⟩=c|0⟩+d|1⟩.

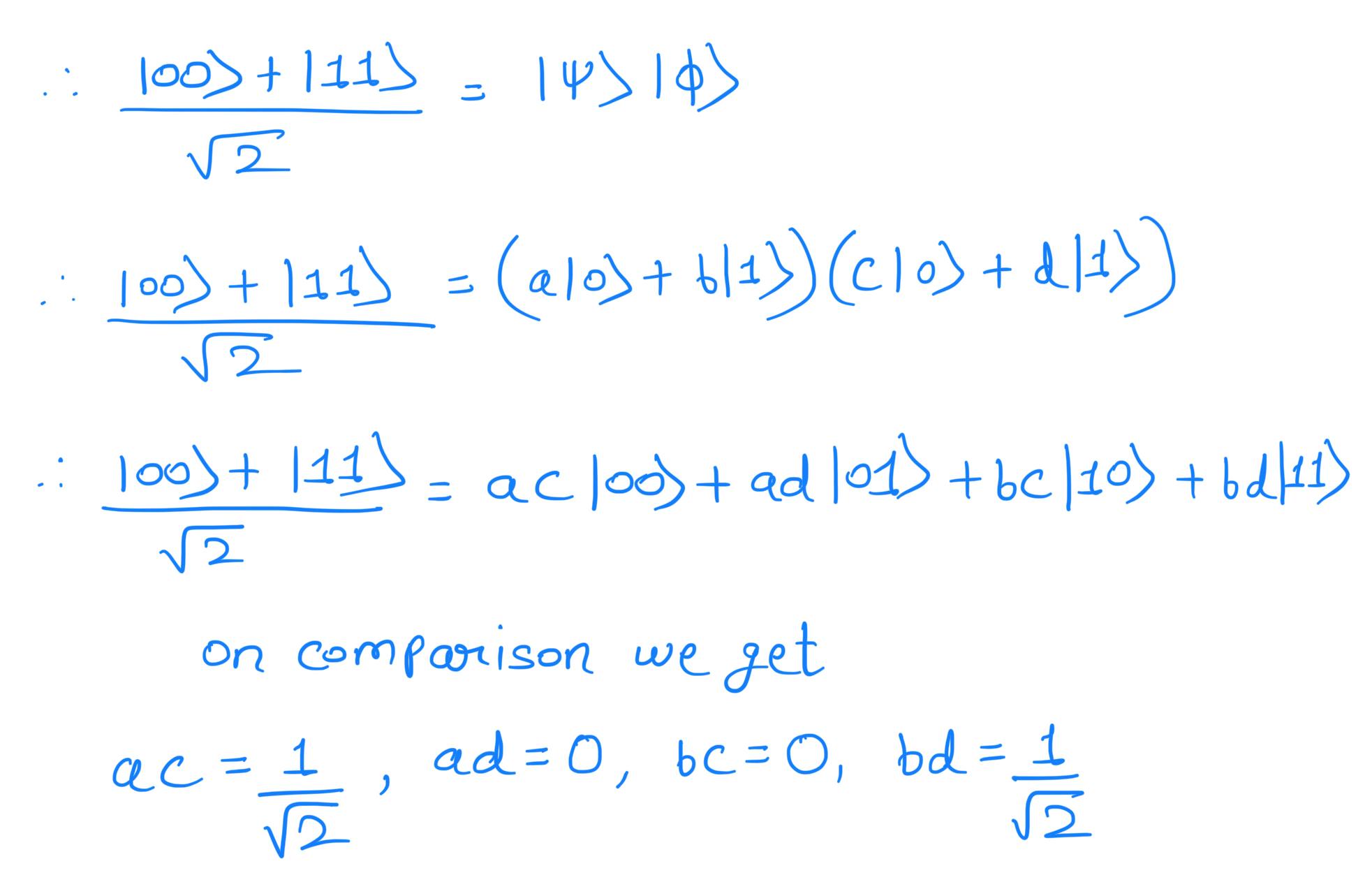
Now

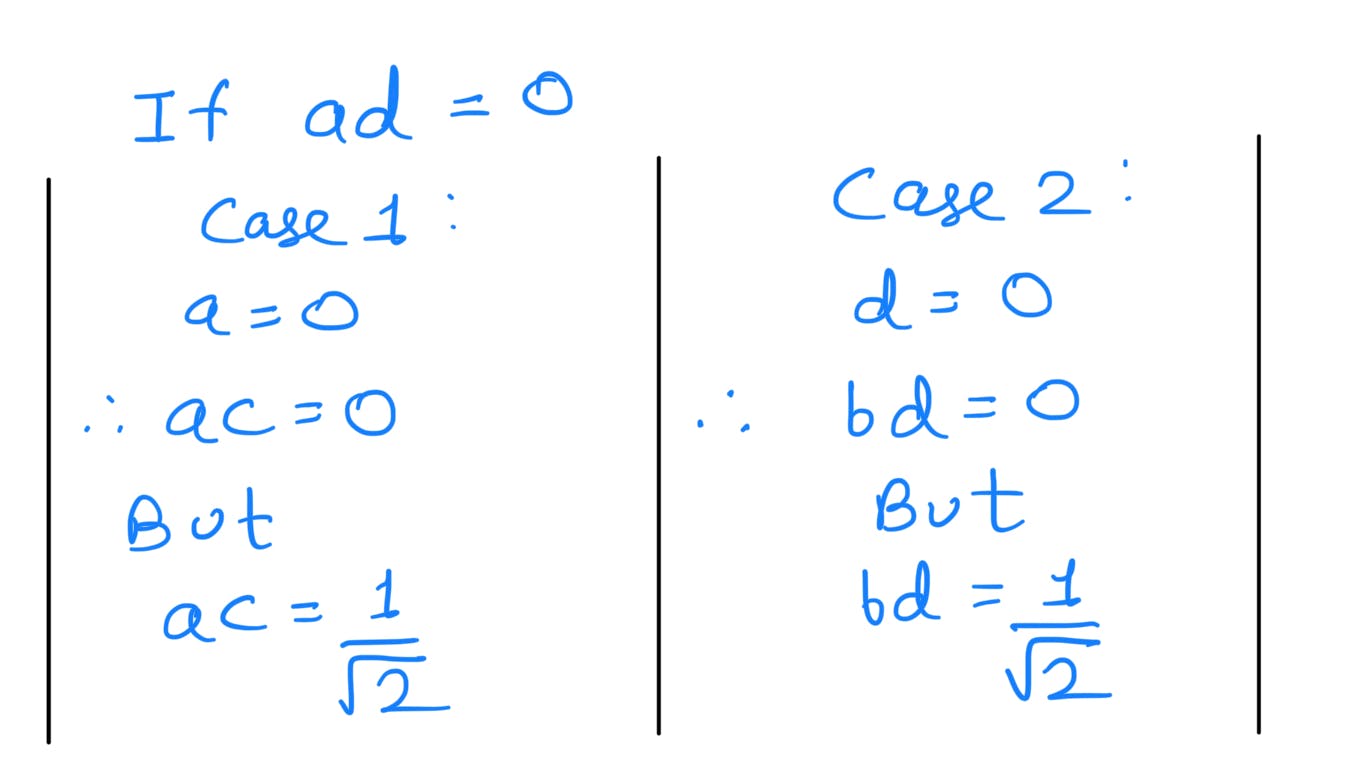
Hence any entangled quantum state cannot be expressed as a tensor product of two quantum states.

Any entangled quantum state is also called a Bell pair or an EPR pair(Einstein-Podolsky-Rosen) pair. John Bell, Albert Einstein, Boris Podolsky and Nathan Rosen pointed out some strange properties of entangled states.

The above-entangled state has the following mnemonic notation:

There are 3 more Bell-pairs or EPR pairs as follows:

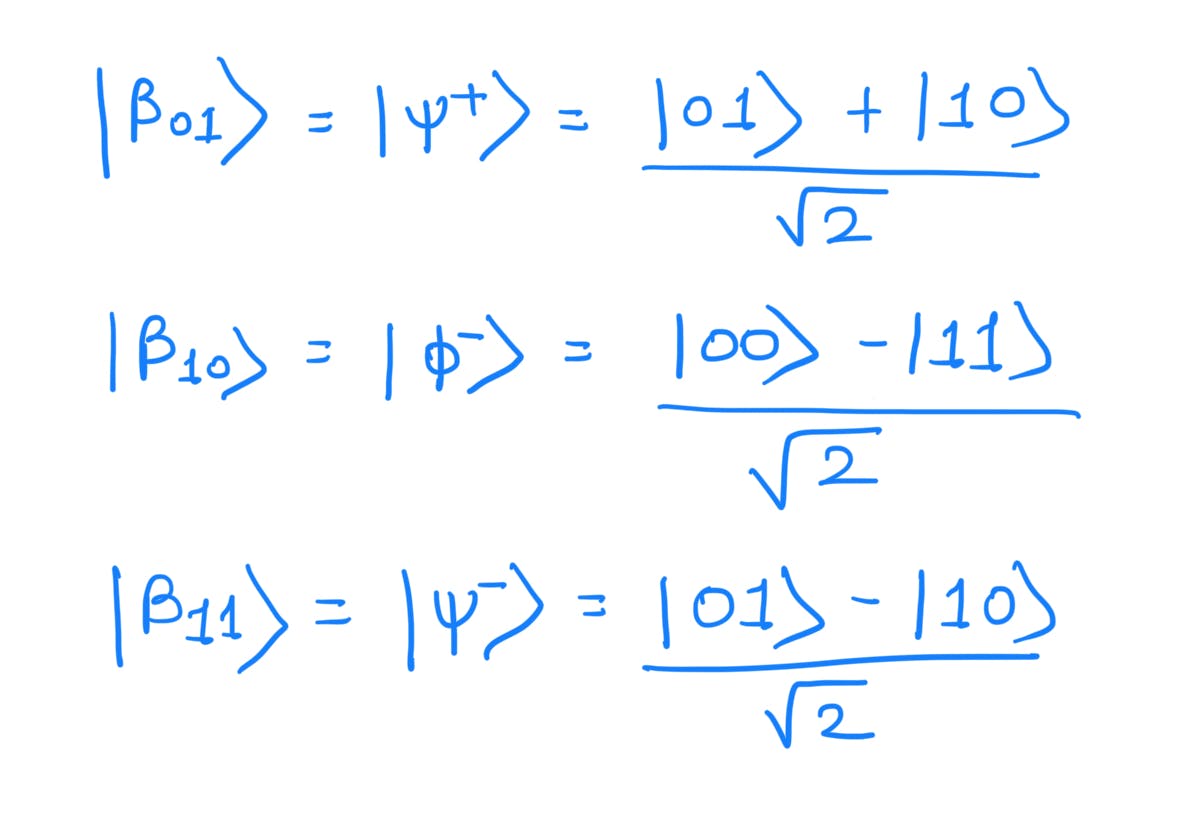
Let's analyze the circuit for these 3 Bell-pairs:

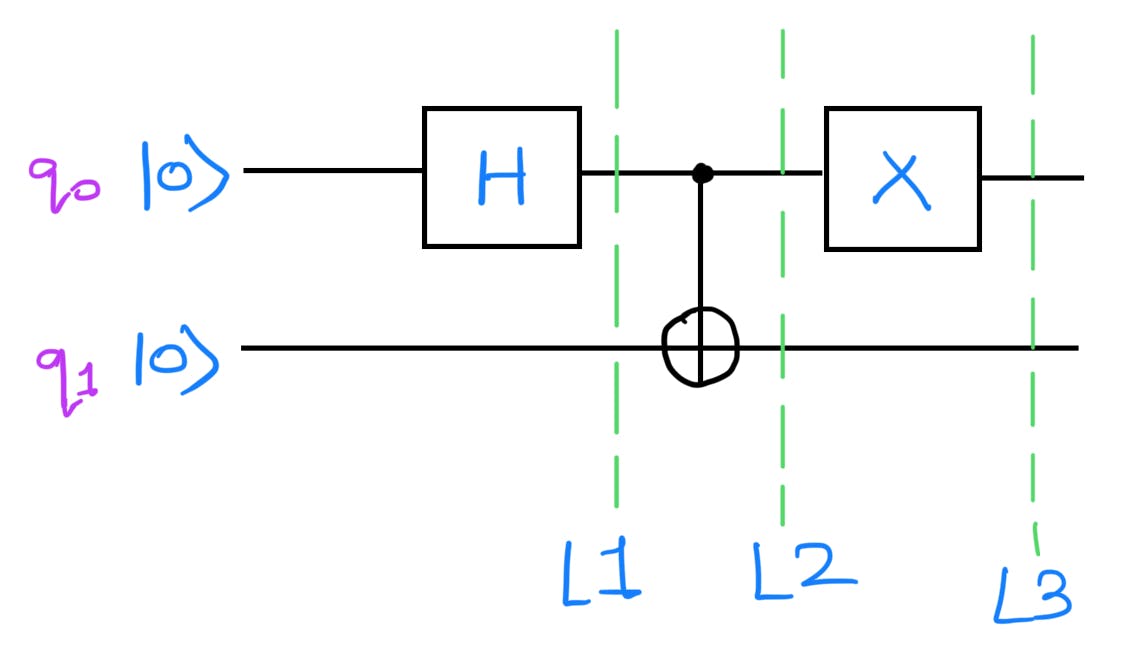
Upto L2 the quantum circuit is the same as the first bell pair quantum circuit. Hence at L2, the quantum state is:

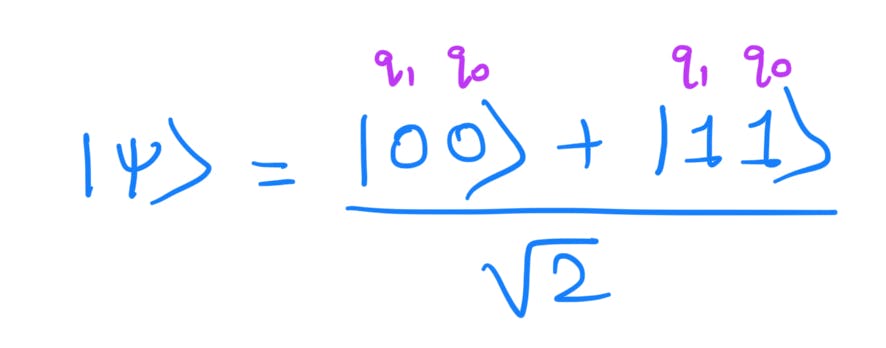
Now applying X gate at q0. Pauli-X gate inverts the qubits i.e. X|0⟩=|1⟩ and X|1⟩=|0⟩.

Hence the quantum state at L3:

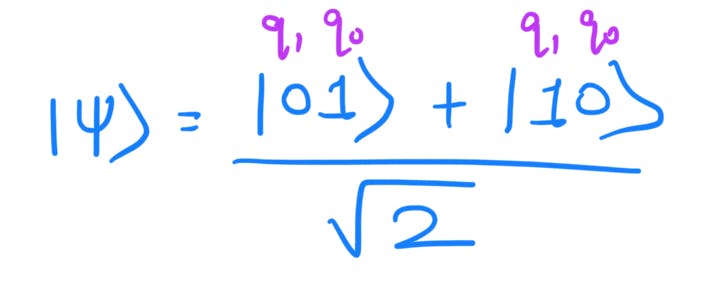
This creates the bell state:

Upto L2 the quantum circuit is the same as the first bell pair quantum circuit. Hence at L2, the quantum state is:

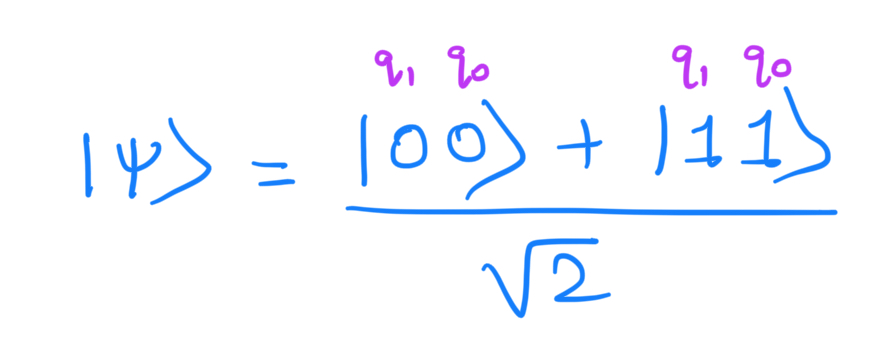
Now applying Z gate at q0. Pauli-Z gate changes the phase of the qubit i.e. Z|0⟩=|0⟩ and Z|1⟩=-|1⟩. When q0=|0⟩ , Z(q0) = |0⟩ and when q0=|1⟩, Z(q0) = -|1⟩. Hence the quantum state at L3 is:

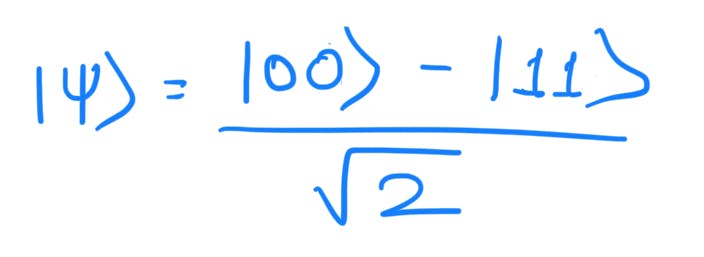
This creates the bell state:

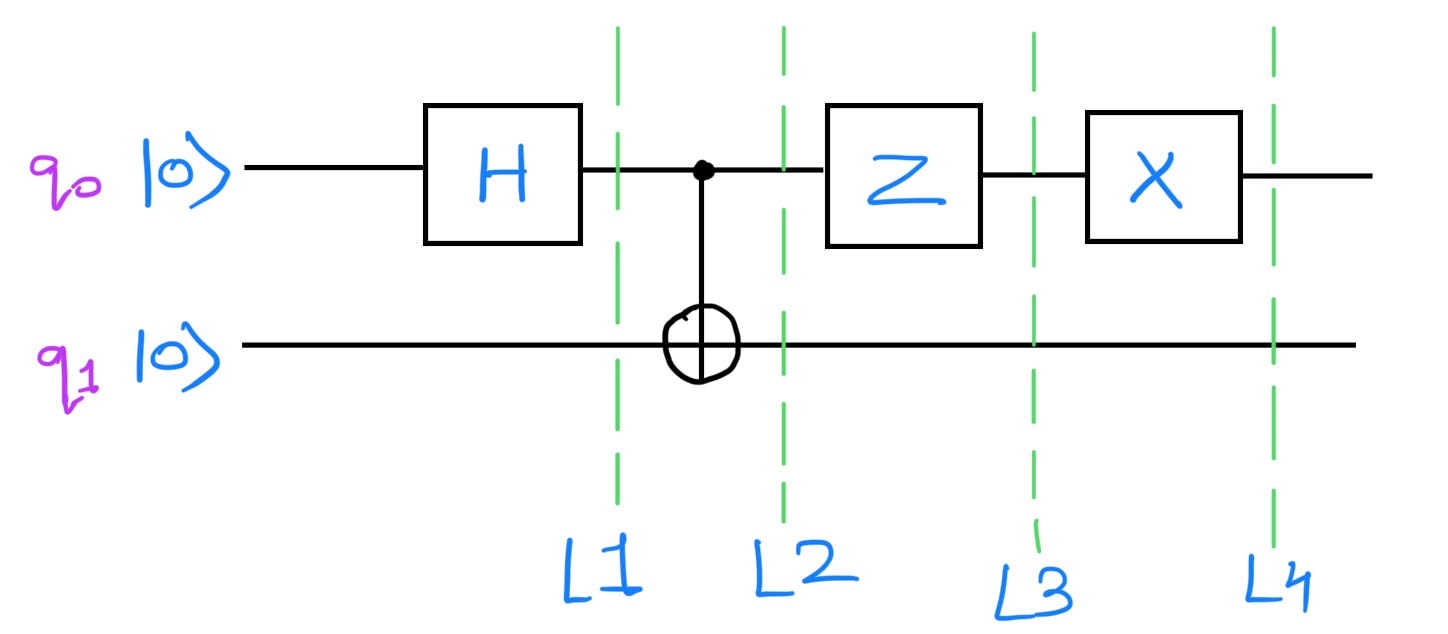
Upto L3 the quantum circuit is the same as the third bell pair quantum circuit. Hence at L3, the quantum state is:

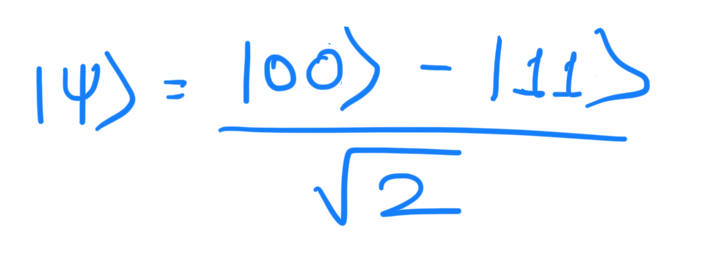
Now applying X gate at q0. Pauli-X gate inverts the qubits i.e. X|0⟩=|1⟩ and X|1⟩=|0⟩. Hence the quantum state at L4:

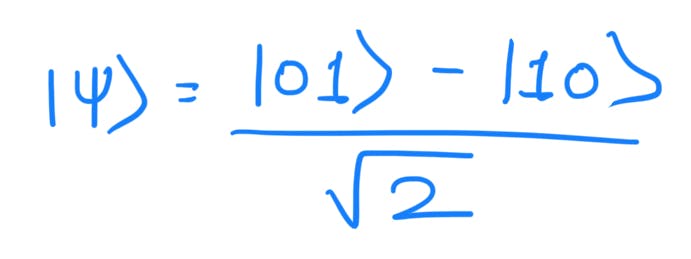
This creates the bell state:

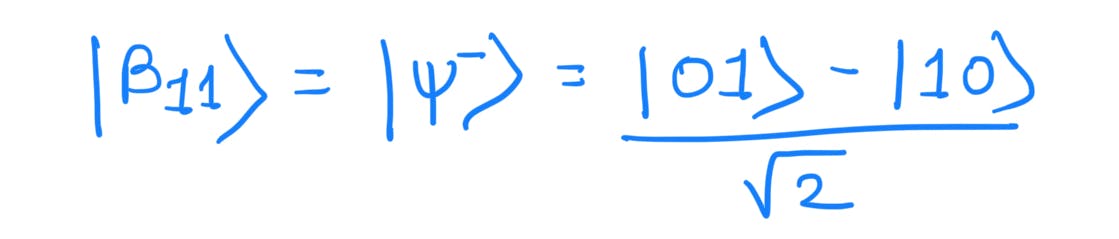
Generalized formula for Bell States:

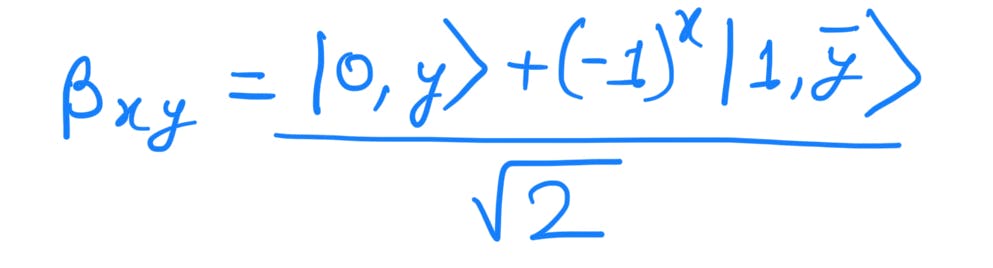
Now entanglement is purely a quantum phenomenon. It is used in cryptography, superdense coding, and quantum teleportation. Consider the state:

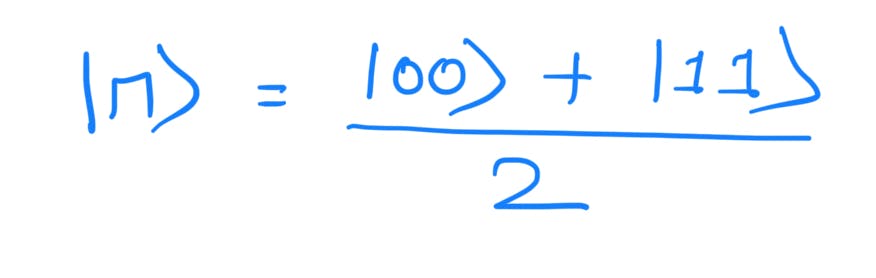
At first glance, it looks like a bell pair or an entangled pair. Even this state cannot be expressed as a tensor product of two quantum states. It is not factorizable. However, this state is not entangled. This state is not even a quantum state.

The basic criteria for a state to be a quantum state is that

• The entries in the vector must be a complex number.

• Euclidean Norm of the entries i.e. the sum of squares of the entries must be equal to 1.

The above state is given by the vector:

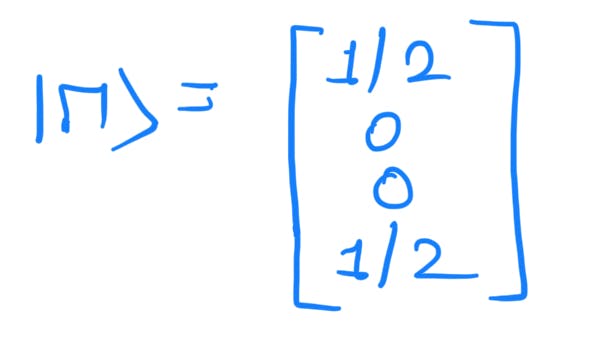
Entries in the vector are real numbers and real numbers are a subset of complex numbers. Hence the first criterion is satisfied.

Let's calculate the norm of the vector:

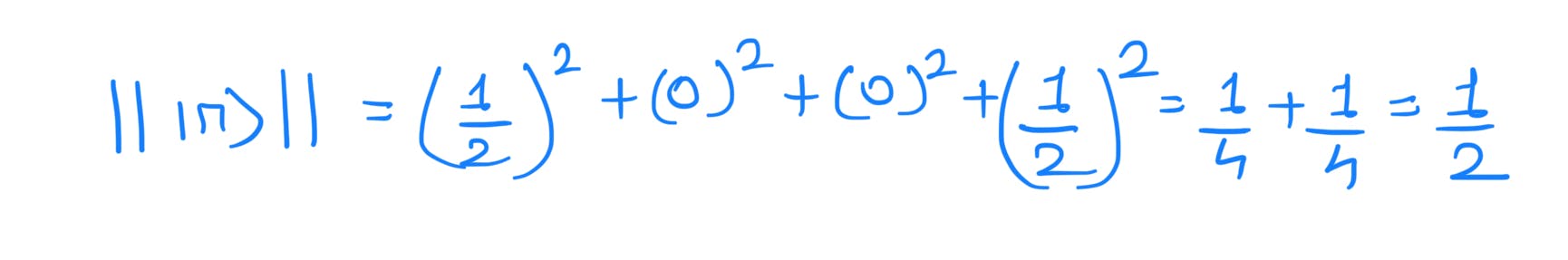
Here the norm of the vector is not equal to 1. Hence it is not a quantum state. Since entanglement is purely a quantum phenomenon, the above state is not entangled.

Ricochet Property or Transpose Trick:

---

Prerequisites:

1)Linear Operators on the space: V⊗W (Tensor product between V and W)

Suppose |v⟩ and |w⟩ are vectors in V and W, and A and B are linear operators on V and W then we can define a linear operator A⊗B on V⊗W by the equation:

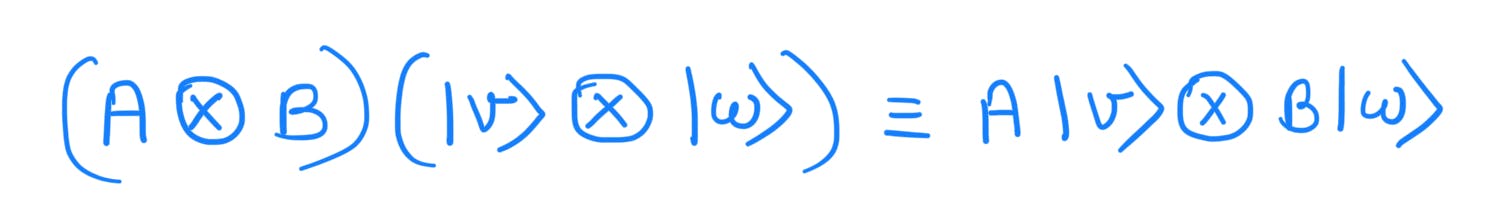
The definition of A⊗B is then extended to all elements of the space V⊗W naturally to ensure the linearity of A⊗B, that is,

2)Unit Impulse Function or Delta function:

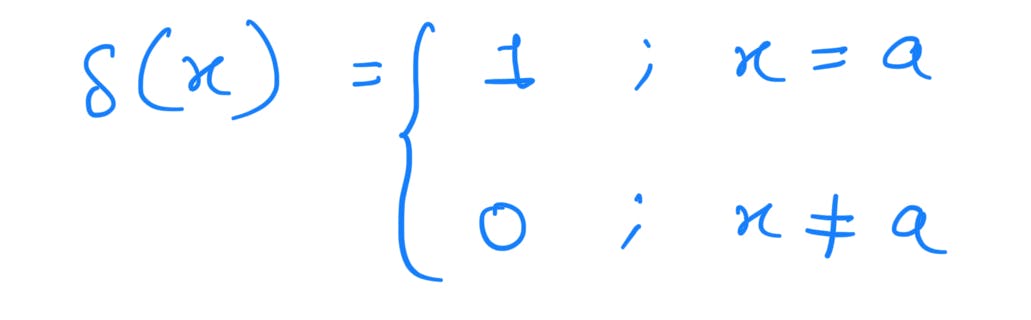
3)The inner product of vectors as delta function:

|0⟩ and |1⟩ are two orthogonal vectors in the Z-basis.

• ⟨0|0⟩=1

• ⟨1|1⟩=1

• ⟨0|1⟩=0

• ⟨1|0⟩=0

If |j⟩ ∈ {|0⟩,|1⟩} and |k⟩ ∈ {|0⟩,|1⟩} then

The above inner product has a structure of delta function.

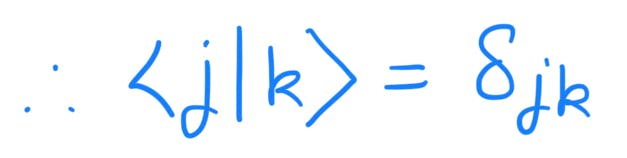
4)Outer Product: A ket vector multiplied by a bra vector.

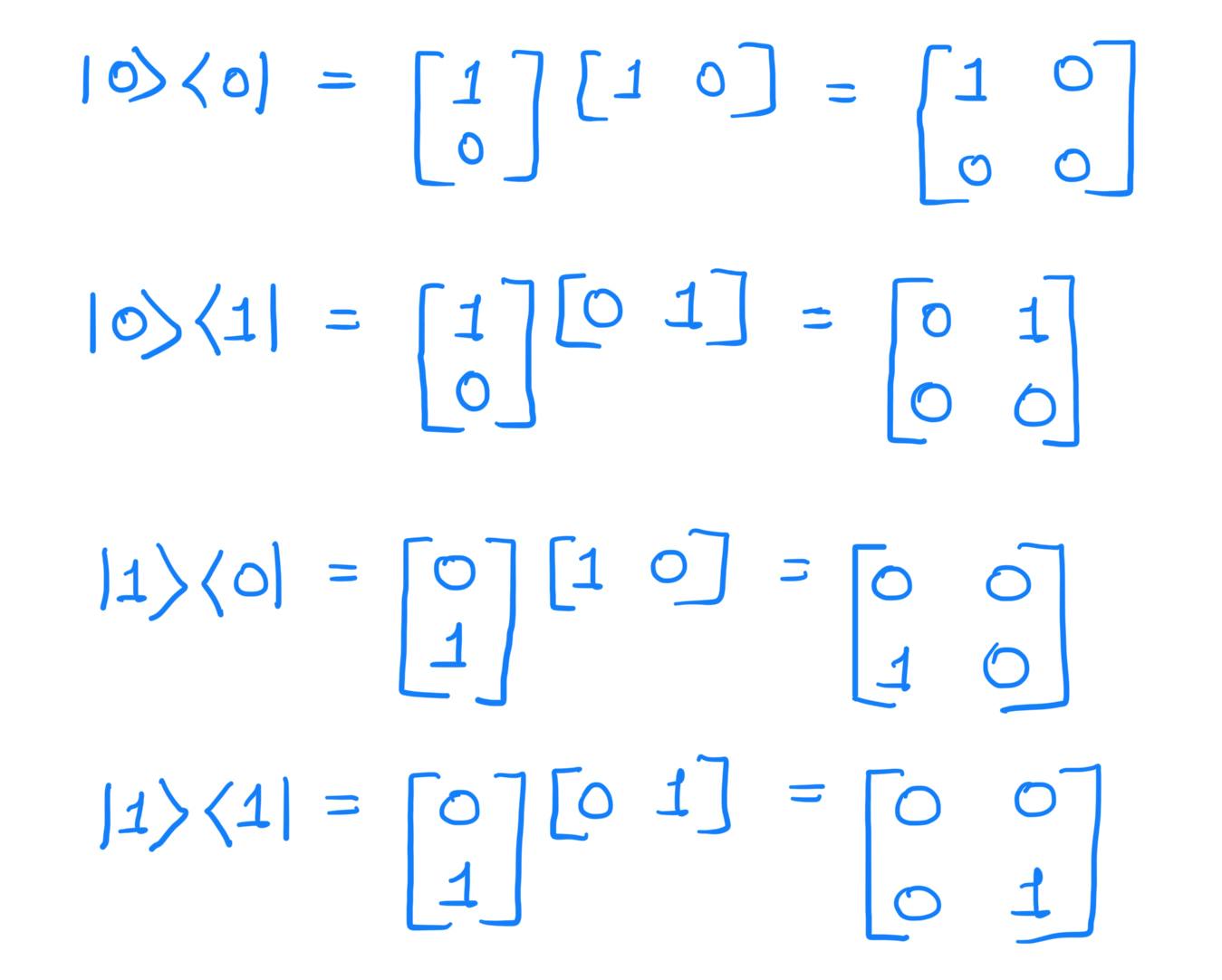
5)Matrix as Sum of Outer Products:

Consider the matrix:

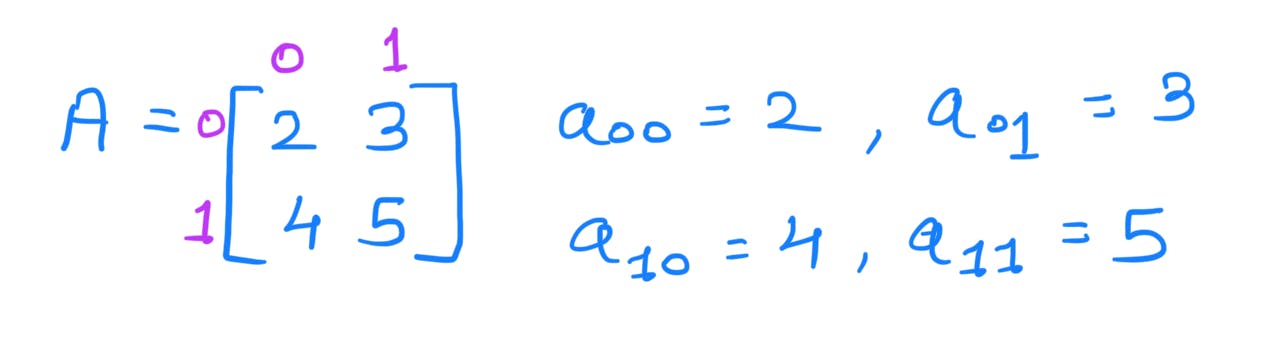
The above matrix 'A' can be expressed as follows:

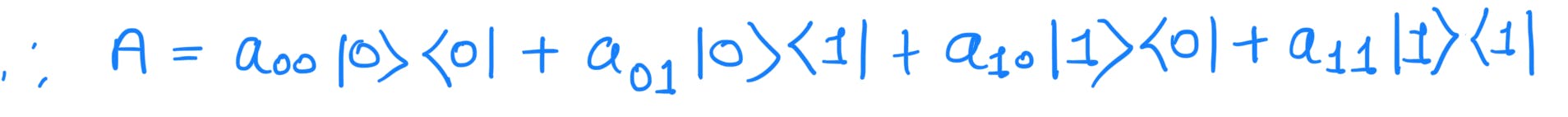
Now consider the transpose of the matrix 'A':

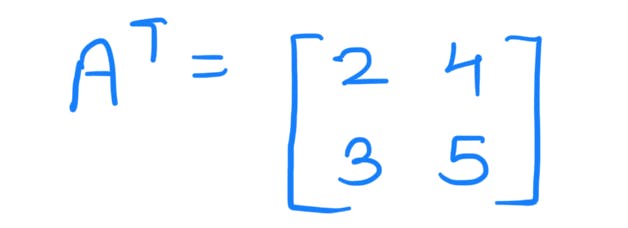
Expanding it as the sum of outer product:

According to the original matrix A the coefficient will be replaced as follows:

---

Ricochet Property:

The ricochet property states that

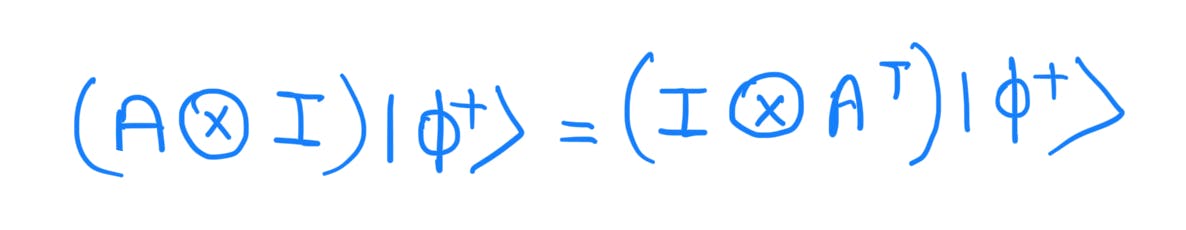
for any matrix (including non-unitary) A acting on any EPR state.

Proof:

We will express the EPR state as follows:

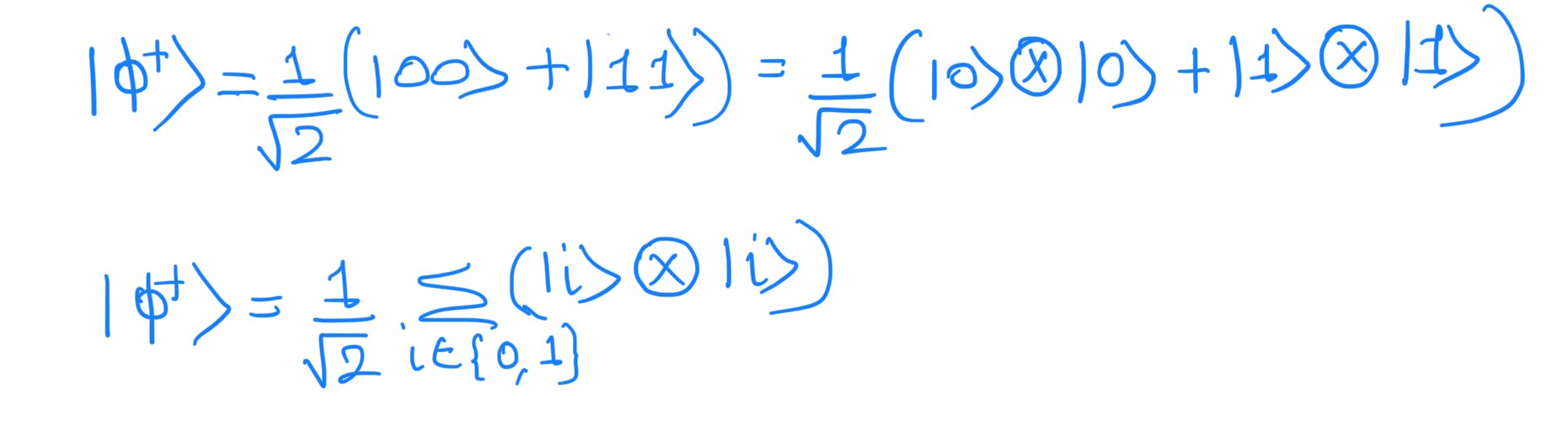
A matrix can be written as the sum of the outer products as mentioned in prerequisite (4). Hence the matrix 'A' will be defined as follows:

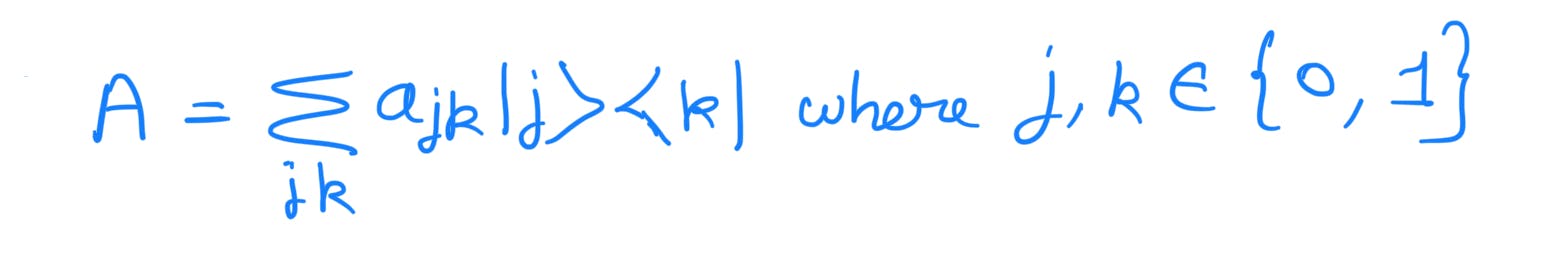
Considering LHS and Prerequisite (1):

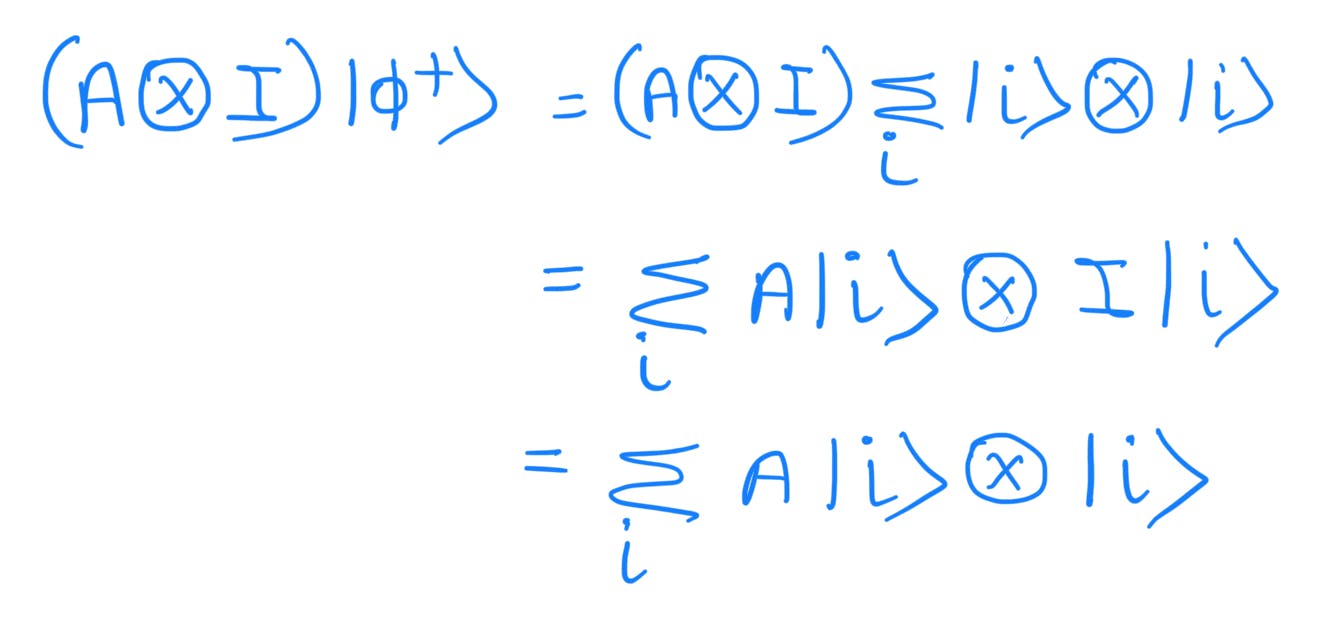
Substituting

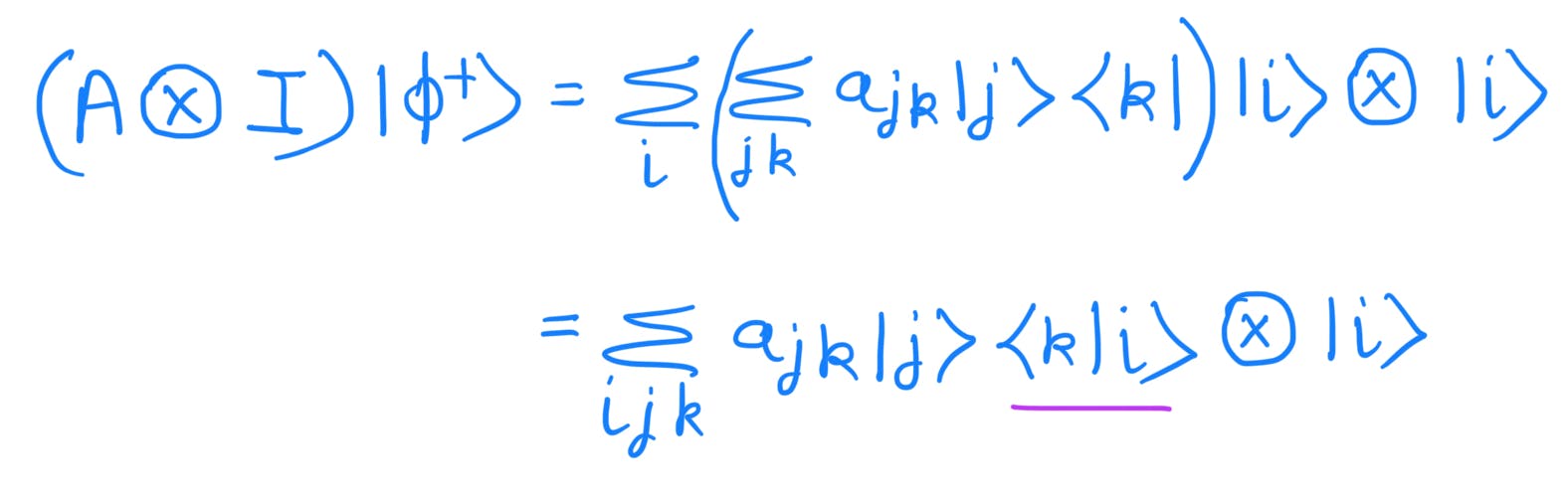
Since k ∈ {0,1} and j ∈ {0,1} the underlined inner product will be a delta function as mentioned in prerequisite (2)&(3).

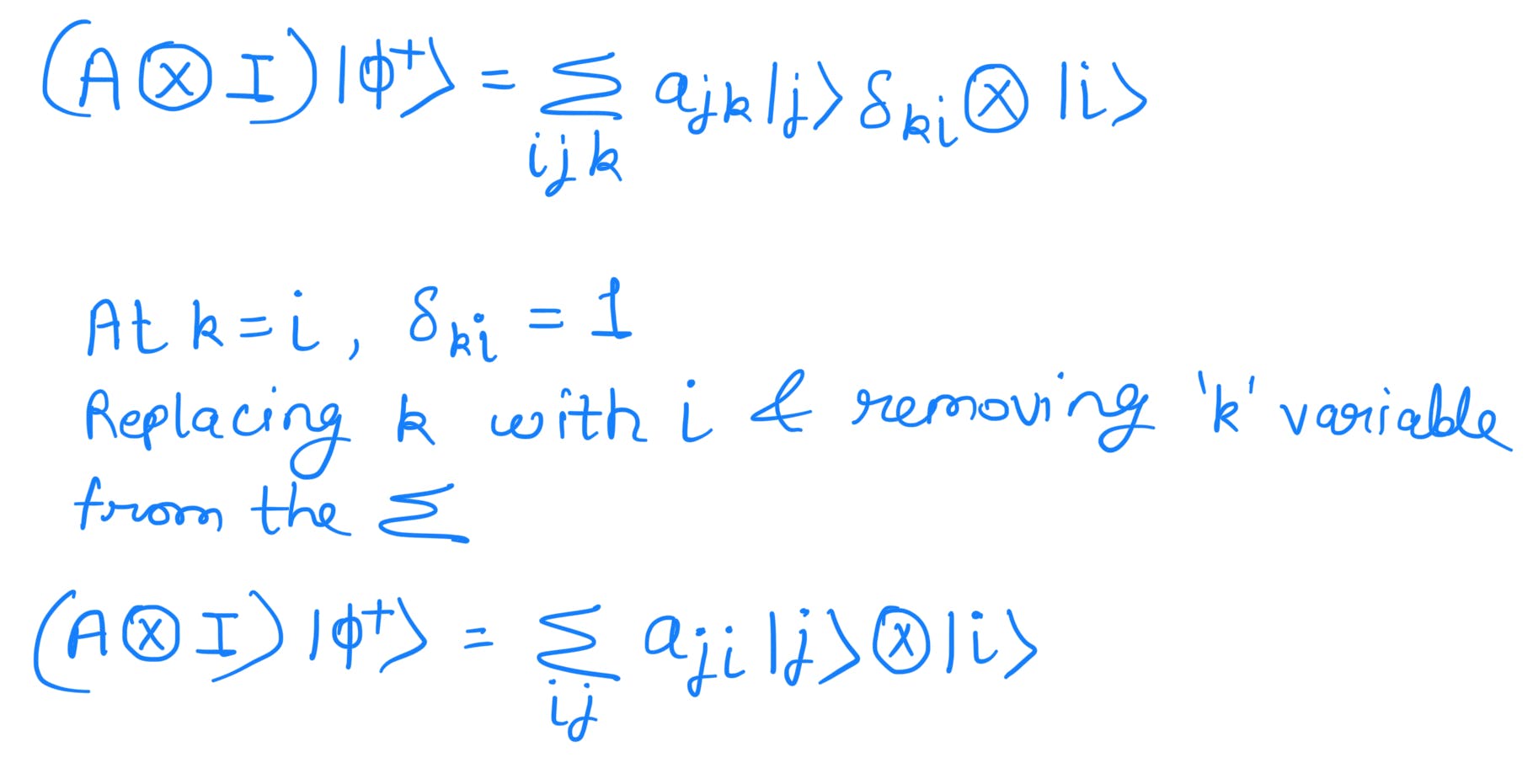
Since summation runs from 1 to n where 'n' is the dimension of the ket vector or the dimension of the operator we can replace i and j.

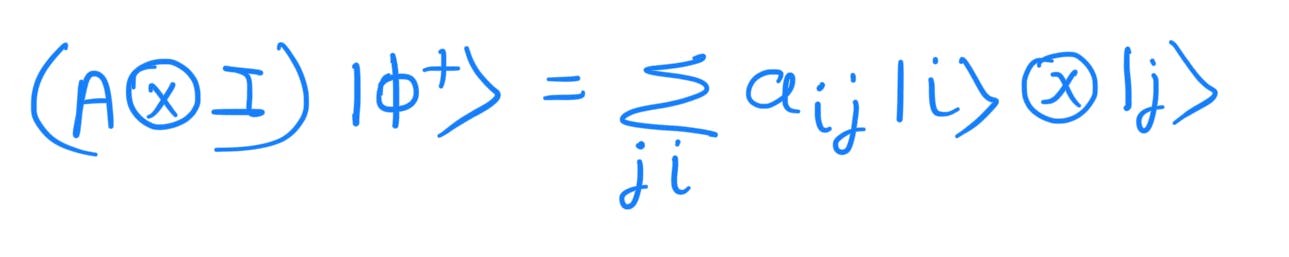
Introducing the delta function to the equation again:

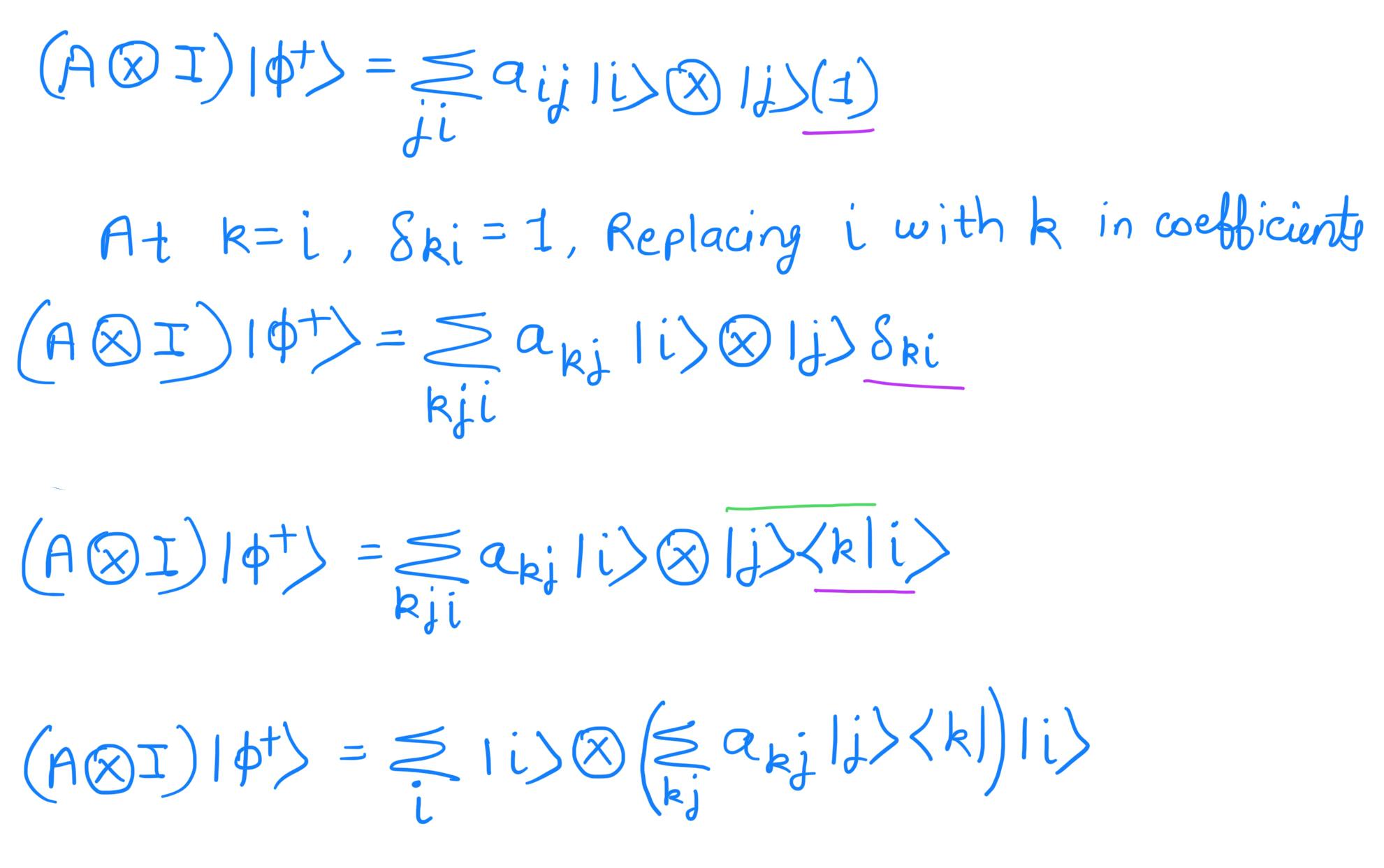
The bracket part is given as the transpose of the matrix A as given in prerequisite (5).

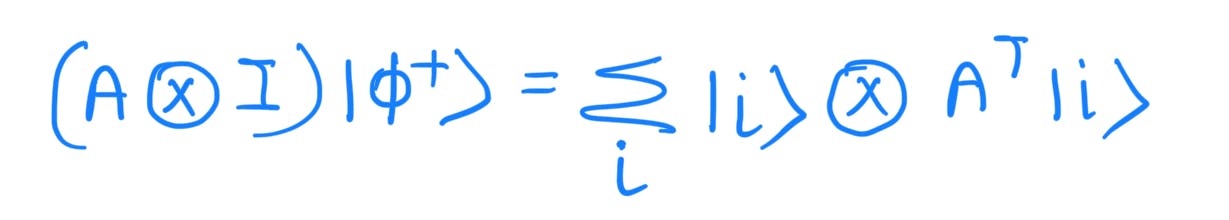
Introducting Identity(I) matrix:

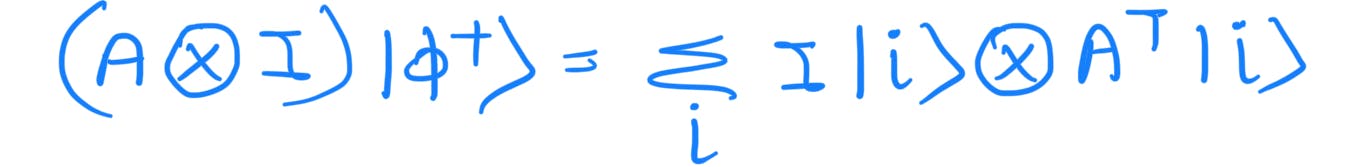
Using prerequisite (1) in reverse order:

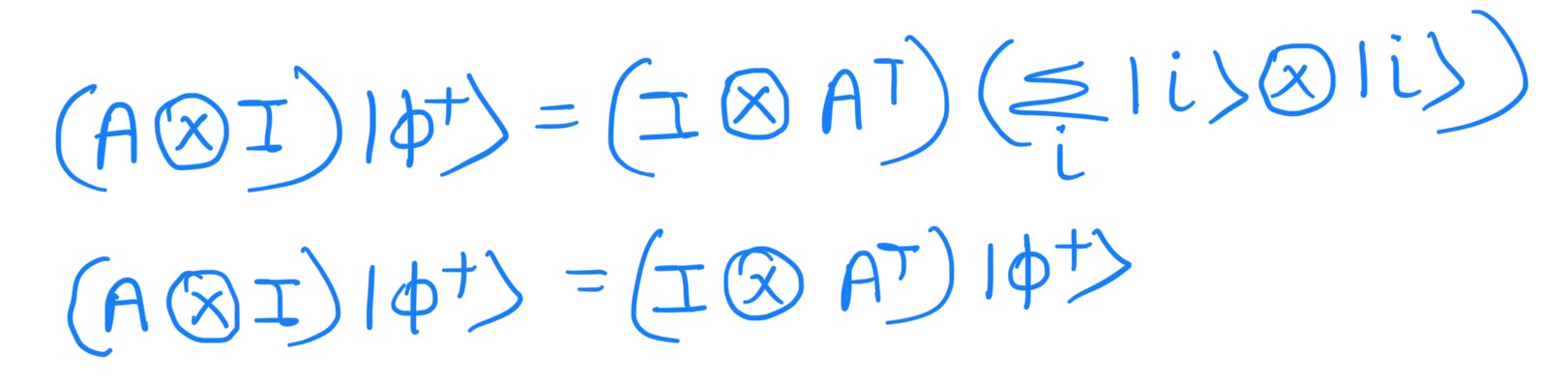
Hence we have proved the ricochet property.

Let's consider an example to see how it works:

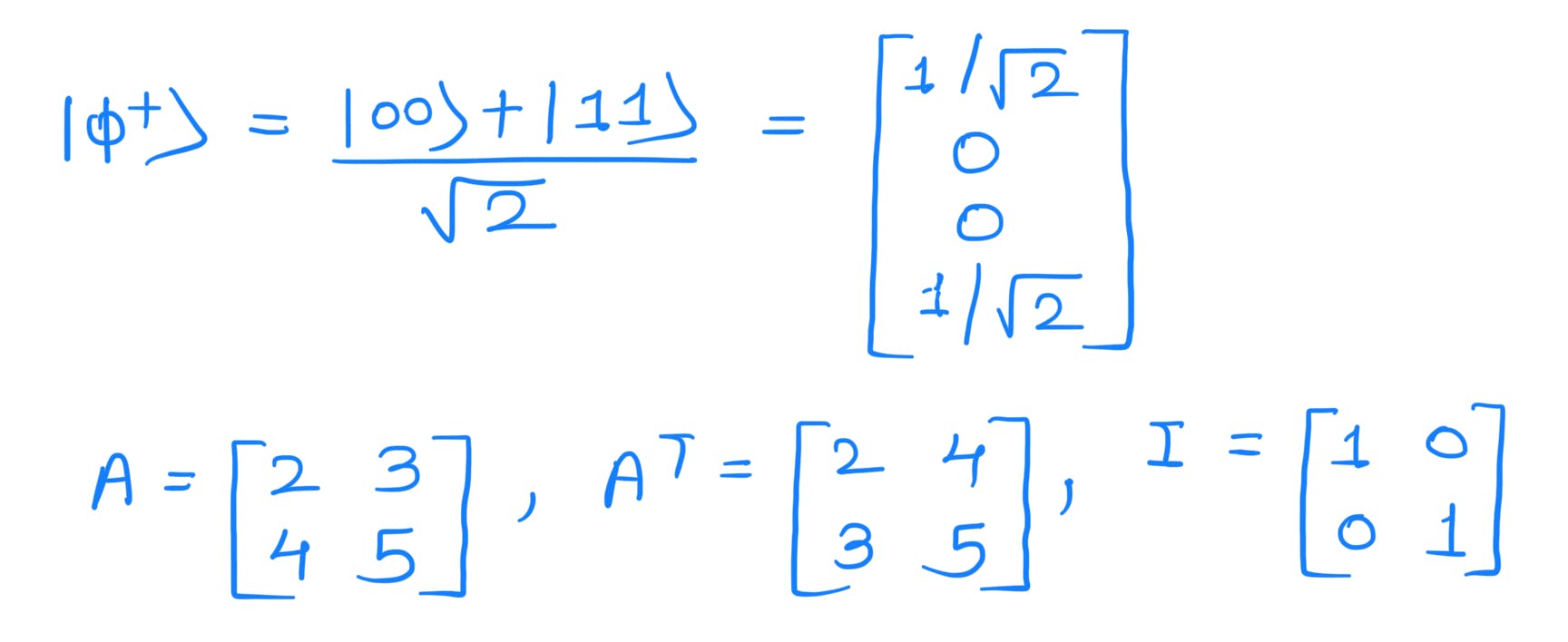
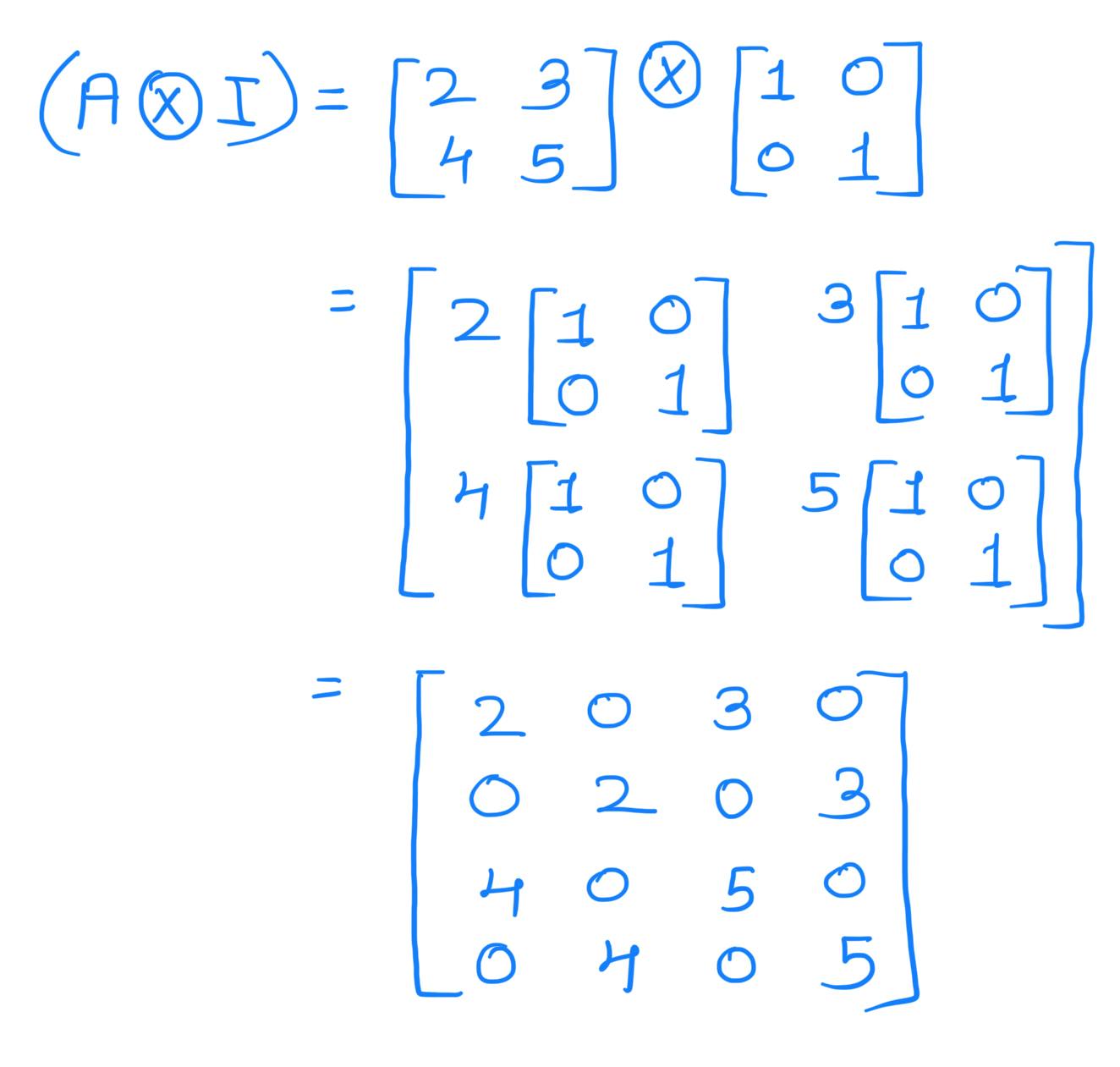
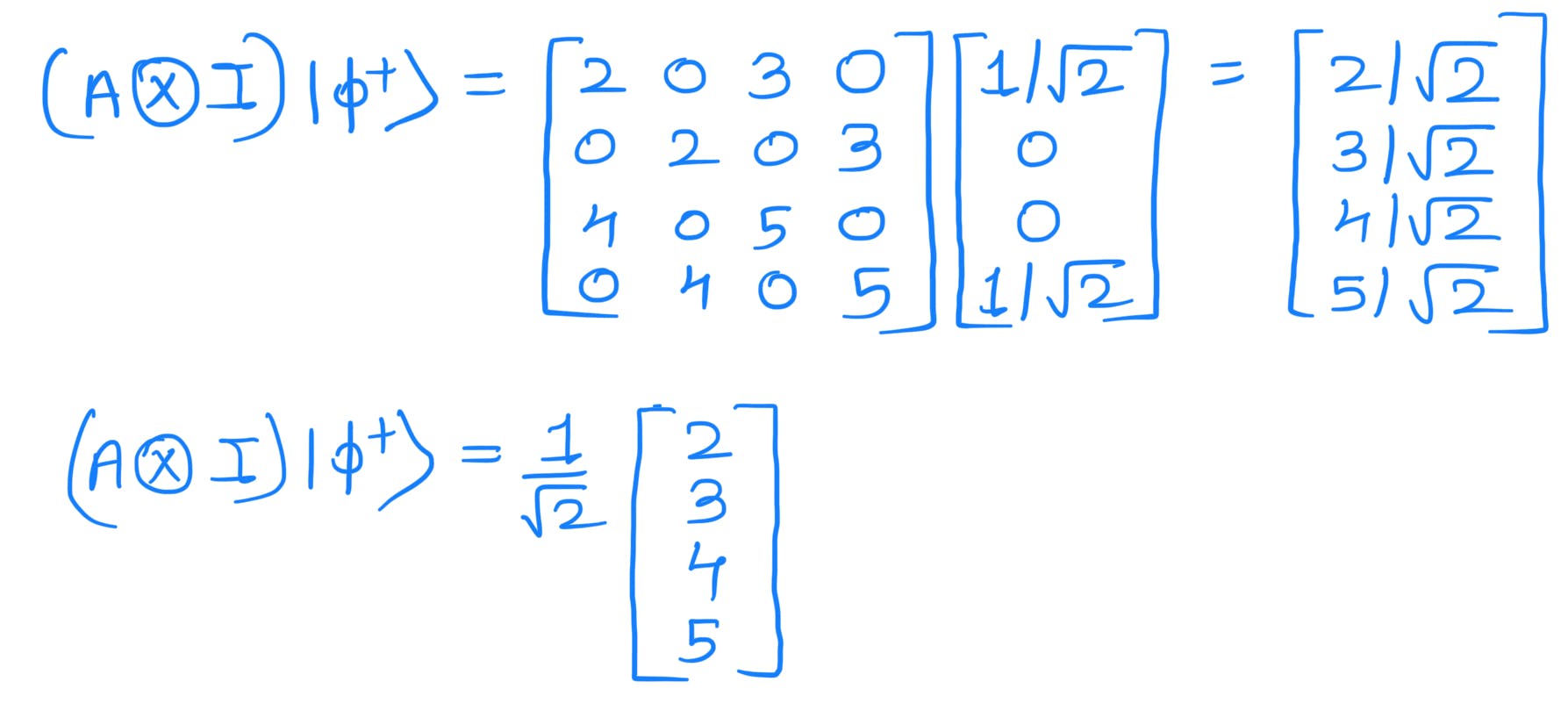
Now

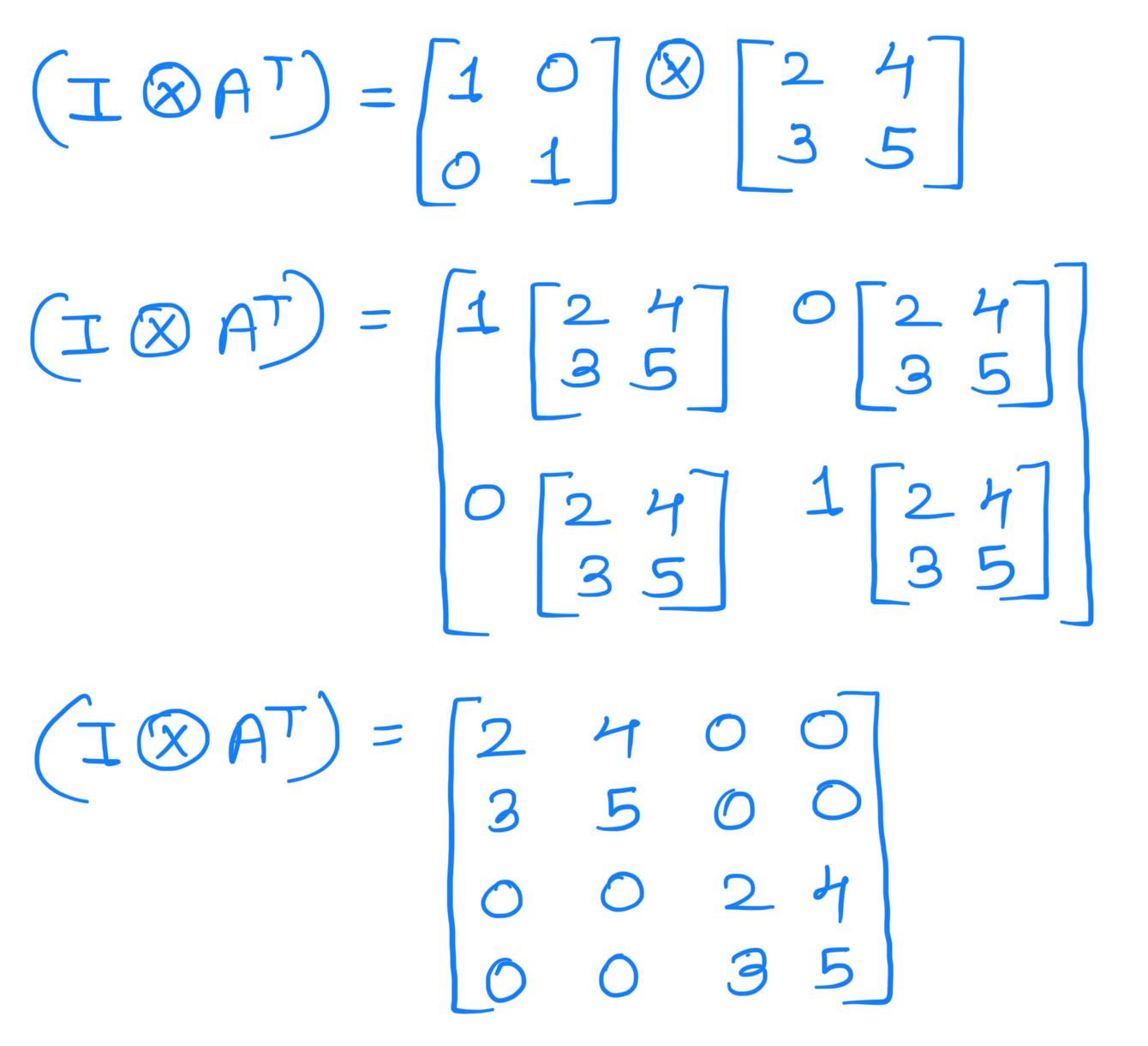
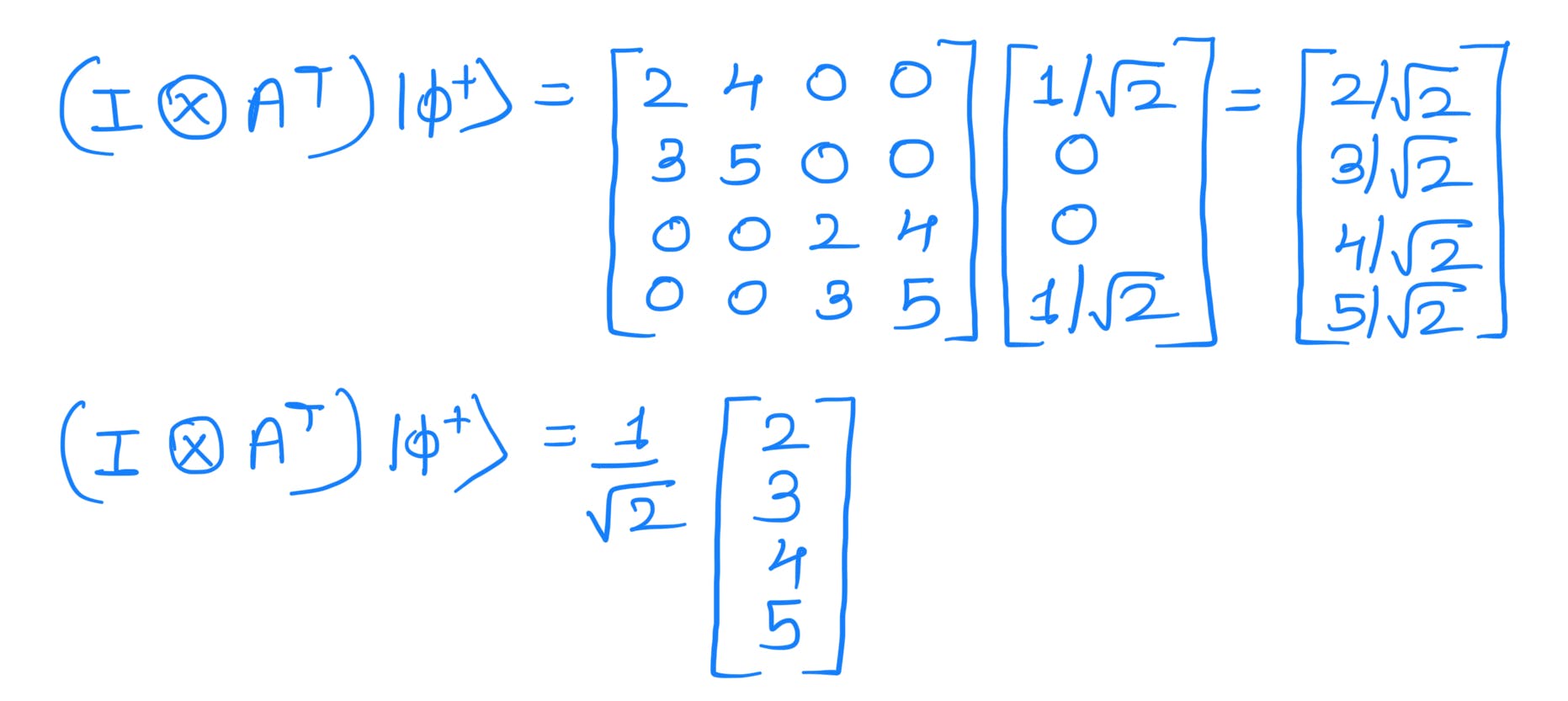
Hence

Qiskit Code For Ricochet Property:

Initial Import Statements: These are auto generated when you start a new notebook on the IBM qiskit lab. We can add few import statements if necessary.

Let's define 'A' as a random unitary matrix:

This 'A_op' is a custom gate. Whenever we want to use such custom gates, we convert the 'random_unitary' into an 'Instruction' using the '.to_instruction()' function. This allows you to use the gate as a building block and insert it into a quantum circuit.

For ricochet property, we also need the transpose of the matrix 'A':

In qiskit, any unitary operator is defined as (Operator at q1) ⊗ (Operator at q0)

Consider circuit:

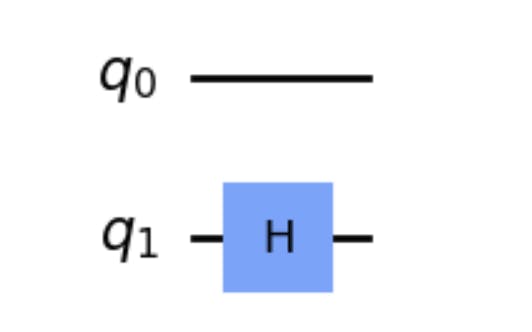
There is no operator at q0, hence the operator at q0 will be considered as an Identity(I) matrix. Hence the unitary operator of the circuit is (H ⊗ I).

Now consider circuit:

There is no operator at q1, hence the operator at q1 will be considered as an Identity(I) matrix. Hence the unitary operator of the circuit is (I ⊗ H).

Now we will prepare the circuit:

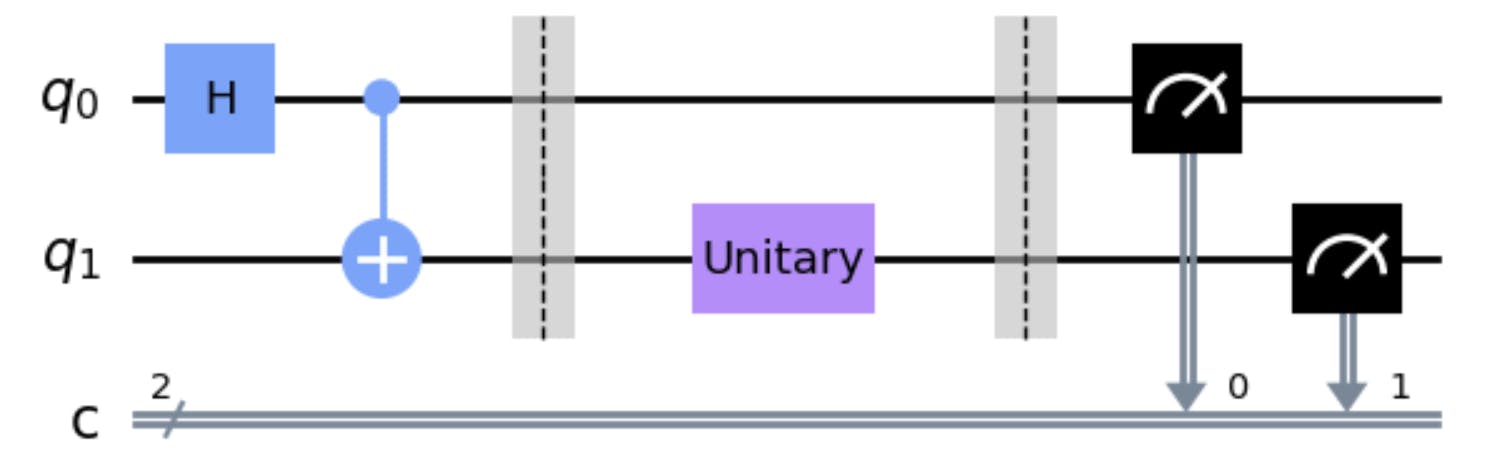
The circuit before the first barrier is the bell state. After the first barrier we have the operator:

Now we will prepare the circuit:

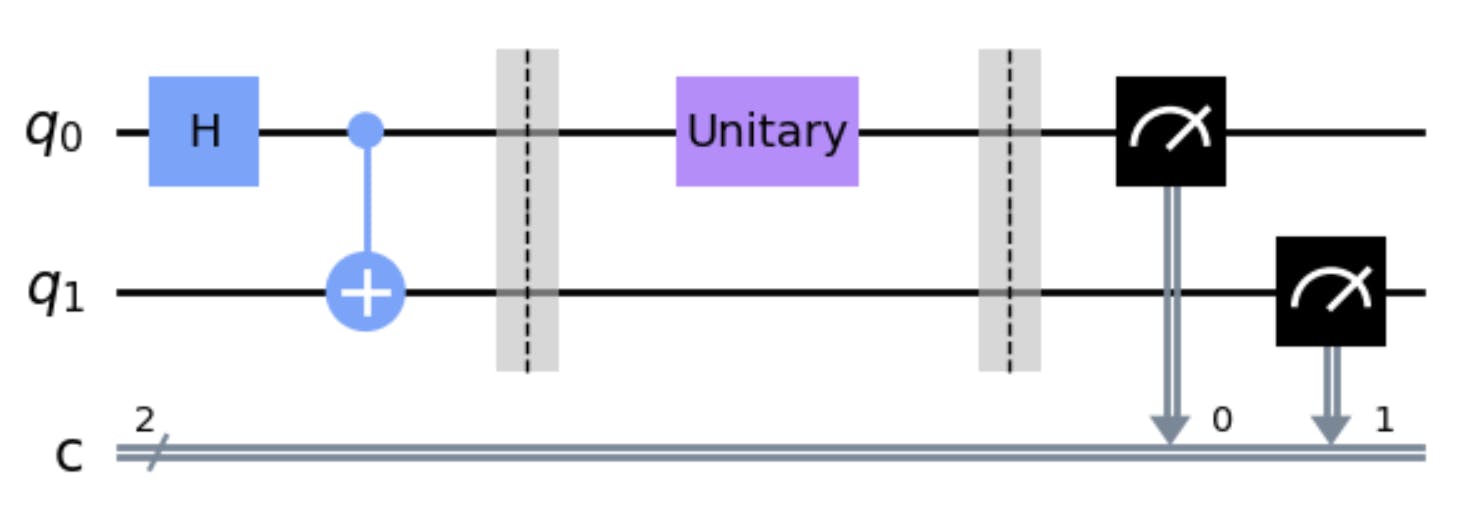
The circuit before the first barrier is the bell state. After the first barrier we have the operator:

Now append these two circuits in a variable qc_list.

AerSimulator: Aer is a high performance simulator for quantum circuits that includes noise models.

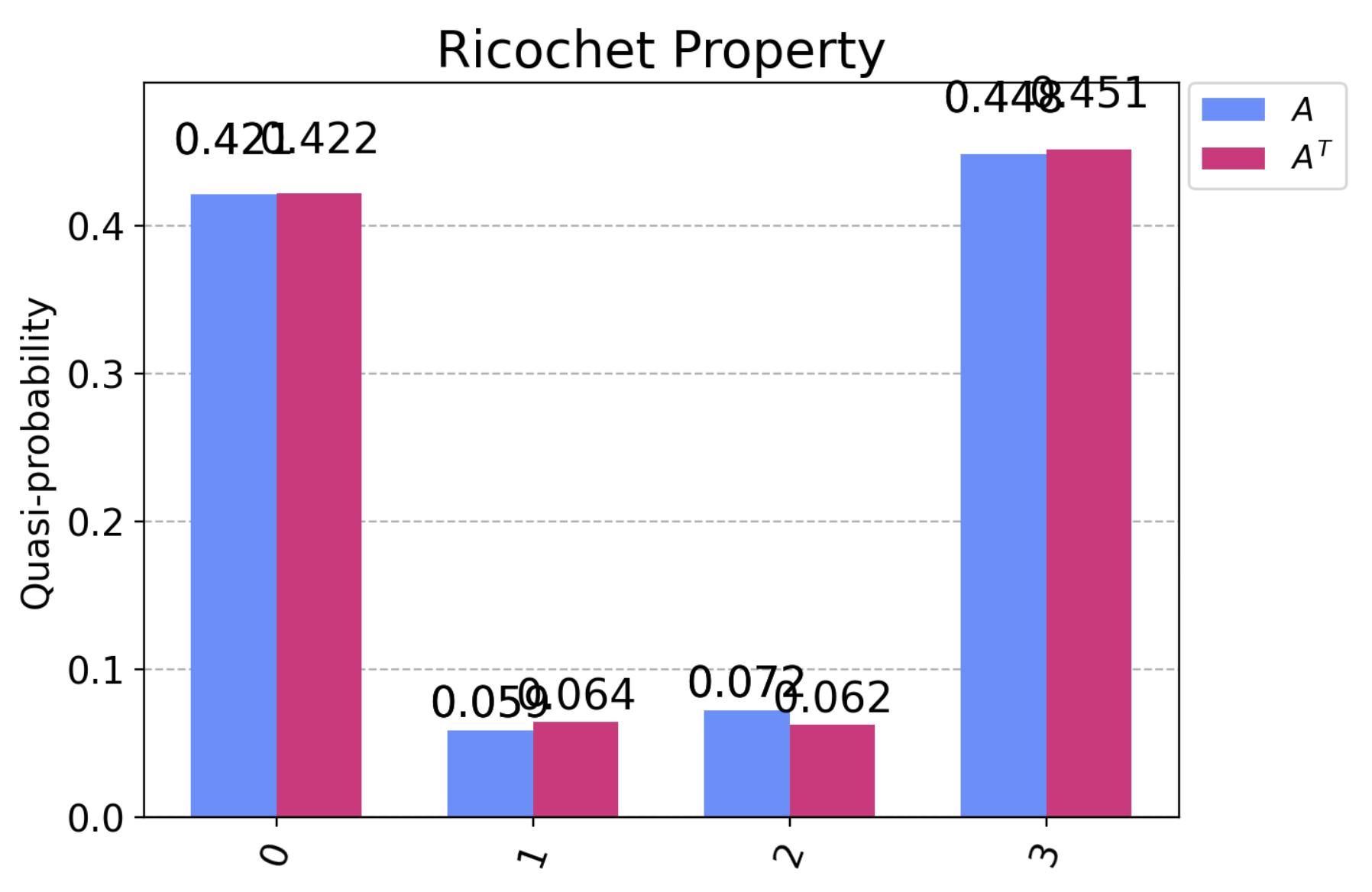
The quasi-probability distribution is a more flexible framework than the classical distribution. If we see the probability distribution, it seems that both the circuit gives the same probability distribution. Hence it satisfies the Ricochet property.

Credit for the above blog:

I have gained the information for the above blog from the book "Quantum Computing and Quantum Information" by Michael A. Nielsen and Isaac L. Chuang, IBM Quantum Explorer's Program, Quantum Information Theory Notes by Nilanjana Datta at University of Cambridge.