"Unclear basics make things complicated!"

Index

• Sets

• Vector

• Dimension of Vector Space

• What is space in mathematics?

  • Euclidean Space

  • Linear Space

  • Hilbert Space

  • Probability Space

• Linear Algebra

• 0-vector in Complex Space

• Vector Subspace

• Dirac Notations

---

A set is defined as a collection of different elements. These objects can be numbers, symbols, points in space, lines, vectors etc. A set may have a finite number of elements or be an infinite set. No two elements in a set can be the same.

E.g.

1)A Set of even numbers between 1 to 10 is given as:

E={2,4,6,8}

It is a finite set.

2)The Set of Natural Numbers is given as:

N={1,2,3,4,...}.

It is an infinite set.

---

In physics, a vector is defined as a quantity with magnitude and direction. But in mathematics(Linear Algebra) a vector is defined as a column matrix. For our purpose, we will consider a vector as only a column matrix.

E.g. Below are some vectors:

---

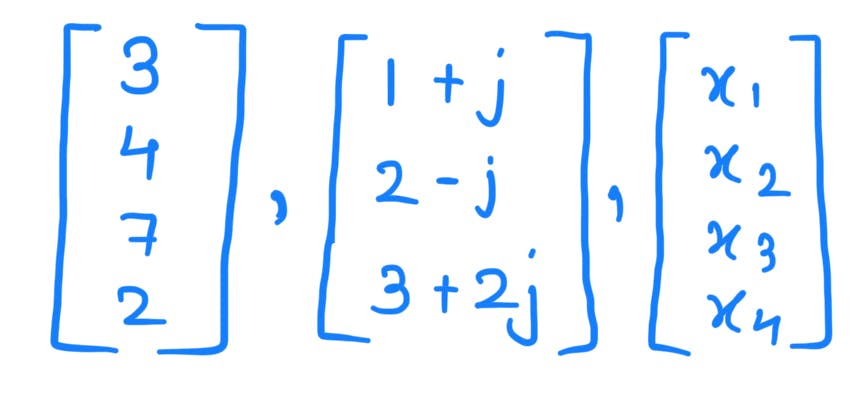
Let's consider the below set:

Each element in this set is a vector and each vector has 3 elements in it. Each element is a natural number. This set can be called a vector space(subspace) of a much larger space. The number of elements in the vector gives the dimension of the larger space in which this set lies. The dimension of the subspace is given by the number of bases that span the subspace. The concept of bases will be explained in further blogs.

Hence the space or set of all possible vectors with 3 elements in each vector and each element a natural number is given as:

---

What is space in mathematics?

In mathematics, a space is a set with some added features like an operation or a relation. Modern Mathematics uses many types of spaces such as:

• Euclidean Space

  It is the fundamental space of geometry. It is intended to represent physical space. It was a 3-dimensional space but there exists Euclidean space with n-dimensional space where 'n' is a positive integer and these are called Euclidean-n spaces.

  

• Linear Space

  A linear space or a vector space is a set whose elements may be a vector. These vectors can be added together or multiplied by a number(scalar). These scalars can be real numbers or complex numbers. Vector spaces generalize Euclidean vectors which allow modeling of physical quantities such as forces or velocities that can have magnitude as well as direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrices, which allows computing in vector spaces.

  

• Hilbert Space

  Hilbert Spaces allow the methods of linear algebra and calculus to be generalized from finite-dimensional space to infinite-dimensional space. Hilbert Space can be considered a Vector Space(Linear Space) of Infinite dimension which is equipped with an inner product. The concept of the inner product will be explained in further blogs.

• Probability Space

  It provides a model of a random process or random experiment. It consists of 3 elements.

  1. A sample space is the set of all possible outcomes.

  2. An event space is a set of events where each event is a set of outcomes in the sample space

  3. A probability function that assigns a probability to each event in the event space.

---

Linear Algebra is the study of vector spaces and linear operations on those vector spaces. A good understanding of Quantum Computing is based on a solid grasp of elementary linear algebra. The chief obstacle to understanding the postulates of quantum mechanics is not the postulates themselves but the concepts of linear algebra and different notations used to represent different quantities in linear algebra.

The basic objects of linear algebra are vector spaces. Consider the vector:

This vector consists of 'n' elements. Consider a set or a space of all such vectors with 'n' complex numbers. This space is given as:

There is an addition operation defined in the above space. It is given as follows:

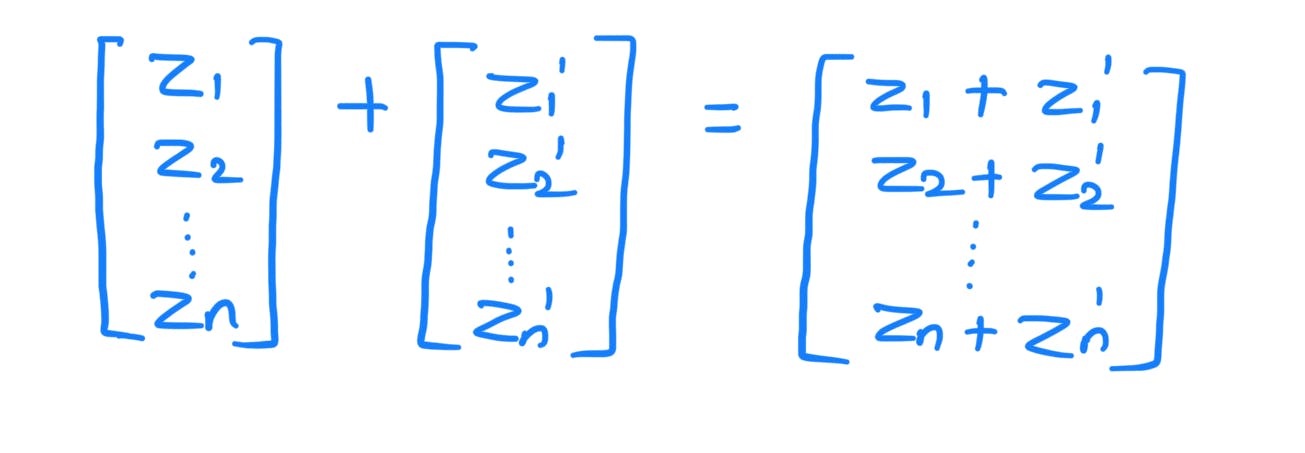
The ith complex number of the first vector is added with the ith complex number of the second vector.

In a vector space, there is a multiplication by a scalar operation. This operation is given as:

The ith complex number of the vector is multiplied by 'z' which is also a complex number.

Since quantum computing is our main motivation to study linear algebra, the quantum mechanical notation for a vector in a vector space is given as:

The above notation is also called a 'ket' which represents a column matrix or a vector.

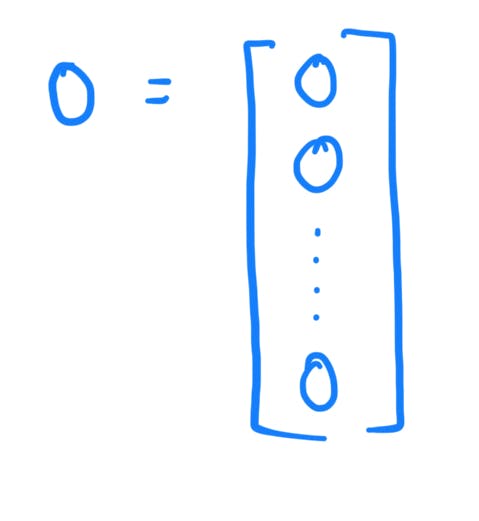
0-vector:

A vector space also contains a zero vector which we denote by 0. It is given as follows:

It satisfies two properties:

• Addition with 0

For any vector |v>:

• Multiplication with 0

For any complex number z:

We do not use ket notation for 0 as |0> means something else in quantum computing.

Vector Subspace:

A vector subspace of a vector space V is a subset W of V such that W is also a vector space i.e. W must be closed under scalar multiplication.

Notations:

• The complex conjugate of the complex number

  

• Vector: ket notation

  

• Vector dual: bra notation

  

• Inner Product

  

• Tensor Product

  

• Abbreviation of Tensor Product:

  

• Complex Conjugate of Matrix:

  

• Transpose of Matrix:

  

• Transposed Conjugate of a Matrix

  

• Inner Product where one operator is operated with a Matrix.

The above style of notation is in general known as Dirac Notation.

Conclusion:

Hence we studied the definition of sets, the definition of vectors, space in mathematics, different types of spaces, the definition of linear algebra, operations on vectors in complex space, 0-vector and its properties, vector subspace and different types of notations used in linear algebra.

Credit for the above blog:

I have gained the information for the above blog from the book "Quantum Computing and Quantum Information" by Michael A. Nielsen and Isaac L. Chuang.